, где I √ энергия ионизации.
Решение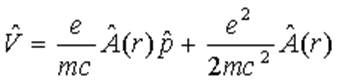 - оператор возмущения.
- оператор возмущения.
Выражения для него было получено в ╧ 13 с тем отличием, что в нашем случае
оператор ![]() имеет вид
имеет вид
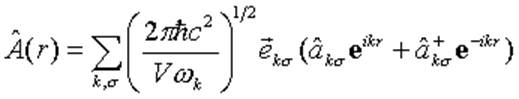
![]() - операторы уничтожения и
рождения фотонов,
- операторы уничтожения и
рождения фотонов,
![]() - вектор поляризации
фотона (
- вектор поляризации
фотона (  -
поперечная волна).
-
поперечная волна).
Система: атом водорода + фотон описывается волновой функцией
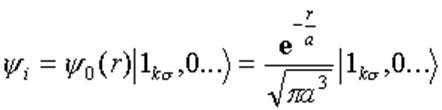 ,
, 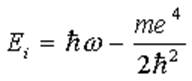 .
.
После поглощения фотона электроном энергия электрона 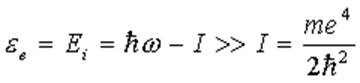 . Следовательно электрон можно считать
совсем свободным. Выбираем в.ф. в виде
. Следовательно электрон можно считать
совсем свободным. Выбираем в.ф. в виде 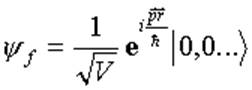 ,
, 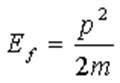 .
.
Вероятность перехода в единицу времени по формуле теории возмущений
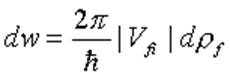 .
.
Член возмущения ![]() описывает двухфотонные переходы, мы его отбрасываем, следовательно ( сейчас
работаем с самой первой формулой)
описывает двухфотонные переходы, мы его отбрасываем, следовательно ( сейчас
работаем с самой первой формулой)
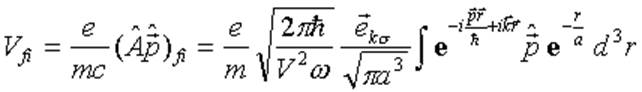
Обозначение: ![]() .
Выберем полярную ось параллельной
.
Выберем полярную ось параллельной ![]() .
.
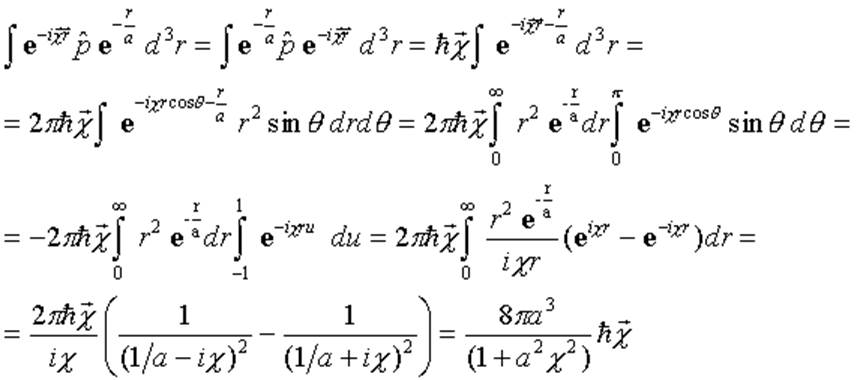
Выше, при написании матричного элемента, мы учли, что
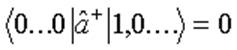
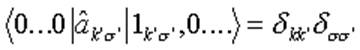 ( ортогональность
различных собственных состояний). Под ⌠учли■ имеется в виду то, что мы
выкинули
( ортогональность
различных собственных состояний). Под ⌠учли■ имеется в виду то, что мы
выкинули ![]() , так как он
не дает вклада в матричные элемент.
, так как он
не дает вклада в матричные элемент.
Вообще, если что, то буквой ![]() везде называлось состояние дискретного спектра (
связанное состояние), а
везде называлось состояние дискретного спектра (
связанное состояние), а ![]() - состояние непрерывного спектра √ свободный
электрон.
- состояние непрерывного спектра √ свободный
электрон.
Кроме матричного элемента в формулу для вероятности перехода входит плотность состояний. Считаем ее.
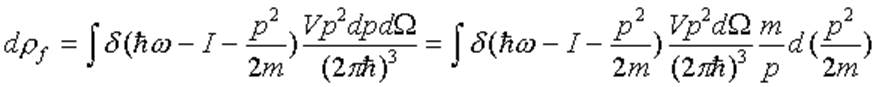 .
.
Здесь d выражает закон сохранения энергии, а дальше все как обычно: объем, умноженный на импульсный объем, и все делится на фазовый объем одного состояния.
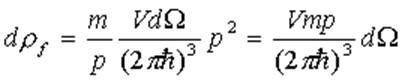
Связь сечения и вероятности: ![]() , значит
, значит
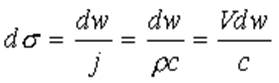
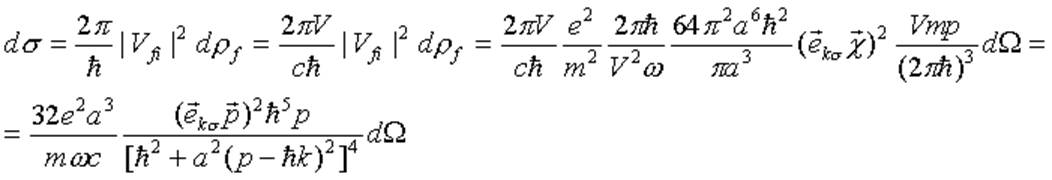 где учтено,
что
где учтено,
что 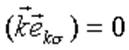 .
.
Выполним усреднение по поляризации фотона
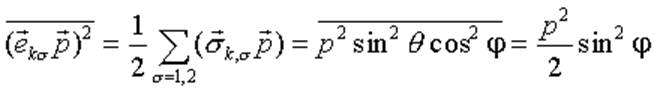
Применимость приближения:
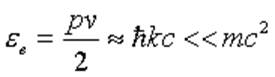 , т.е.
, т.е. ![]() ,
, ![]() .
.
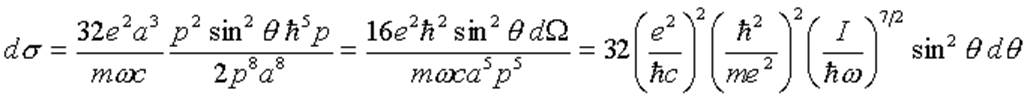
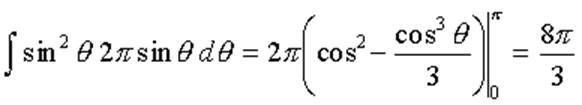
Полное сечение: 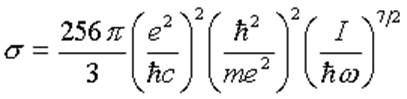
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.