
![]() Решение УШ
для атома (одноэлектронное приближение)
Решение УШ
для атома (одноэлектронное приближение)
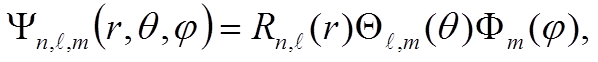
где
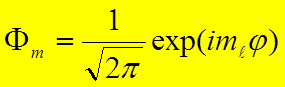 ,
, ![]() –
собственная функция оператора проекции орбитального момента.
–
собственная функция оператора проекции орбитального момента.
![]() Линейная комбинация :
Линейная комбинация :
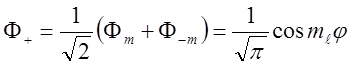 ,
,
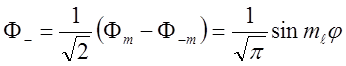 ,
,
также является решением УШ.
|
|
|
|
|
|
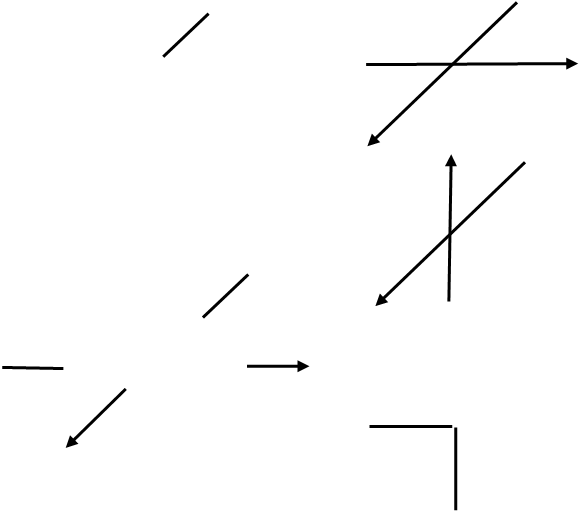
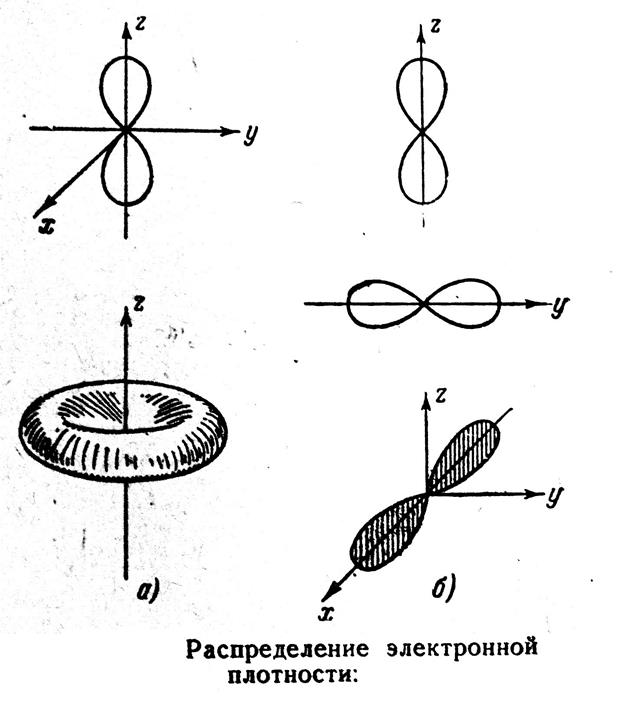
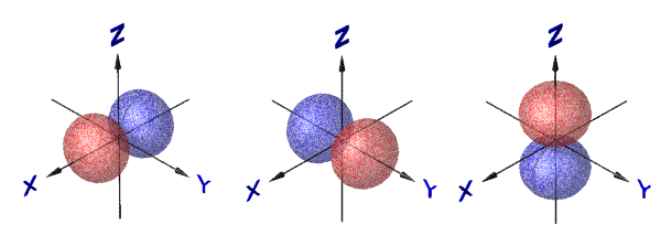
Пример n = 2, ![]() = 1
= 1
![]()
|
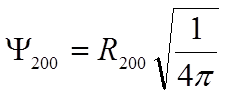 ,
,
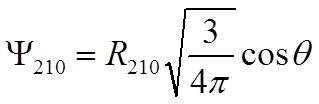 ,
,
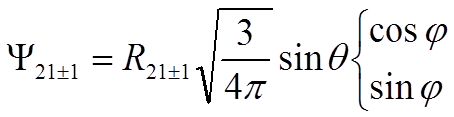 .
.
![]()
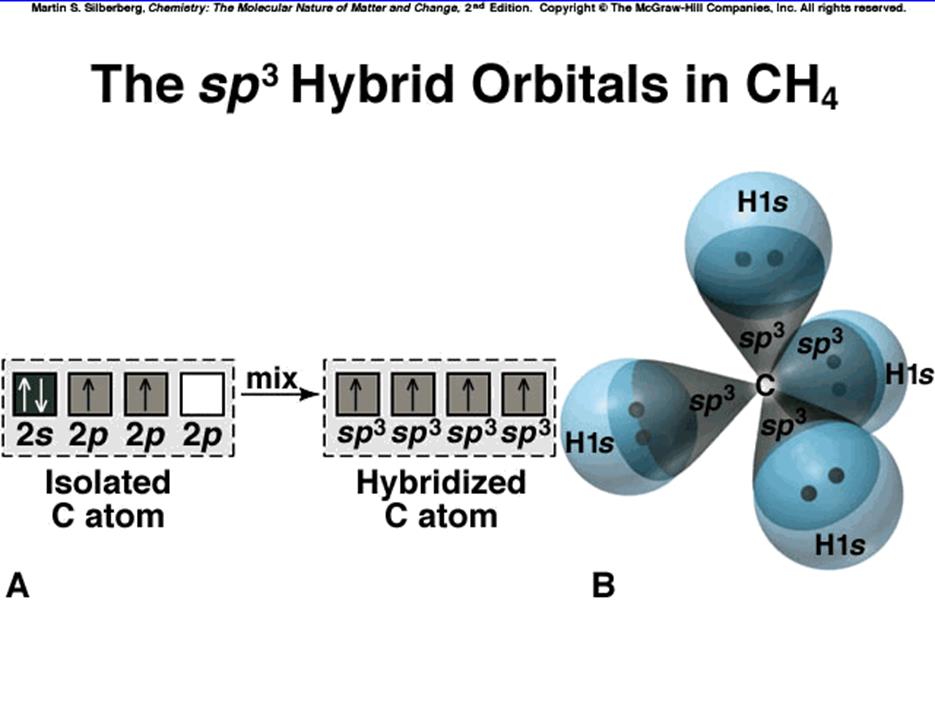
Гибридизация (на примере углерода в молекуле метана)
![]() атома углерода:1s22s22p2
Þ валентность 2 (молекула СН2 ).
атома углерода:1s22s22p2
Þ валентность 2 (молекула СН2 ).
![]() как правило она равна 4 (напр. СН4)
как правило она равна 4 (напр. СН4)
![]() можно объяснить возбужденным состоянием:
2s2p3 - валентность 4. Ошибка! Ошибка связи.однако получим плоскую
молекулу (!) а не тетраэдр
можно объяснить возбужденным состоянием:
2s2p3 - валентность 4. Ошибка! Ошибка связи.однако получим плоскую
молекулу (!) а не тетраэдр
![]() очевидно, что s - орбиталь
и три px,y,z - орбитали не могут создать четыре
равноценные связи тетраэдра.
очевидно, что s - орбиталь
и три px,y,z - орбитали не могут создать четыре
равноценные связи тетраэдра.
![]() Это состояние можно представить линейной
комбинацией собственных ВФ:
Это состояние можно представить линейной
комбинацией собственных ВФ:
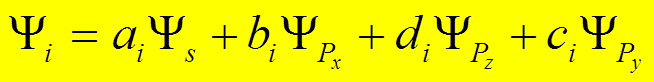 ,
i = 1,2,3,4
,
i = 1,2,3,4
при условии максимума энергии связи в молекуле.
![]()
![]() нормировка и
ортогональность дают:
нормировка и
ортогональность дают: 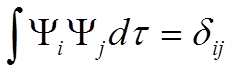 Þ
Þ
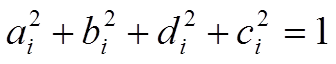
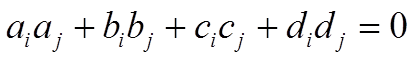 .
.
![]()
![]() пусть связь направлена
пусть связь направлена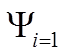 вдоль Х.
Тогда (
вдоль Х.
Тогда (![]() )х
= (
)х
= (![]() )х = 0 Þ
)х = 0 Þ
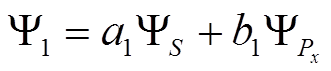
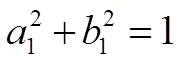 , Þ
, Þ
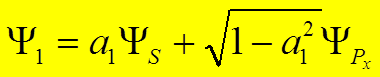 .
.
![]()
![]() предположим, что радиальные
предположим, что радиальные 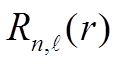 не зависят
от
не зависят
от ![]() , тогда нормируя *
на
, тогда нормируя *
на 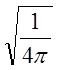 , получим
, получим
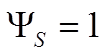 ,
, 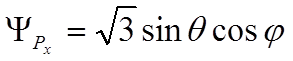 ,
, 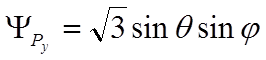
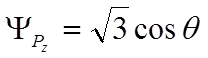 .
.
![]()
![]() учитывая, что вдоль X
учитывая, что вдоль X ![]() получим
получим
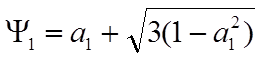 .
.
![]()

![]() условие максимальной связи
условие максимальной связи ![]() Þ а1 = ½, b1 =
Þ а1 = ½, b1 = ![]() /2
/2
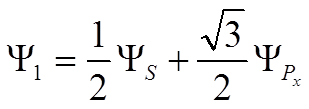 .
.
![]()
![]()
![]() далее, расположив
вторую линию связи в плоскости xz, где
далее, расположив
вторую линию связи в плоскости xz, где 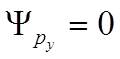 , аналогично найдем
соотношения
, аналогично найдем
соотношения 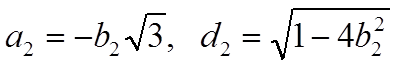 и, учтя, что
и, учтя, что ![]() ,
получим
,
получим
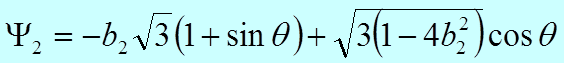 ,
,

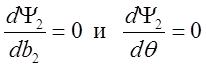 дают
дают 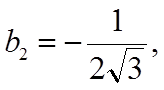
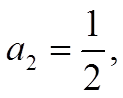
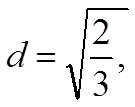
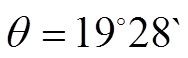 .
.
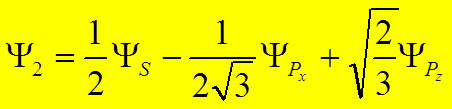
![]()
![]() угол между первой и второй гибридной связью
угол между первой и второй гибридной связью
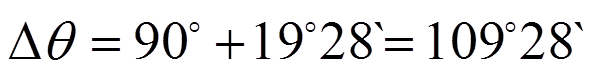 ,
,
равный тетраэдрическому углу (!).
 Аналогичным
образом можно получить
Аналогичным
образом можно получить
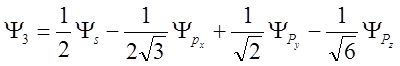 ,
,
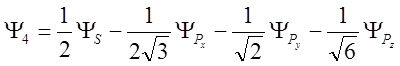 .
.
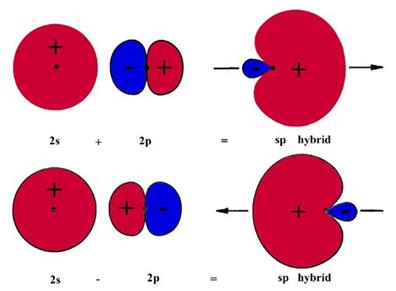
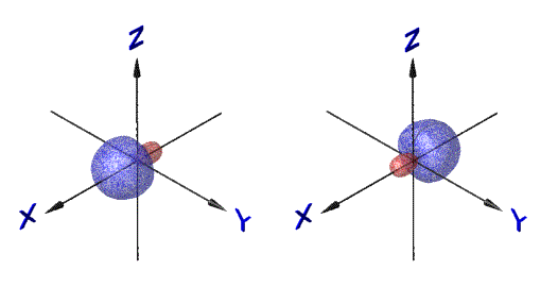
Итак, линейная комбинация
(гибридизация) ![]() собственных функций приводит к
образованию тетраэдрически ориентированных собственных функций.
собственных функций приводит к
образованию тетраэдрически ориентированных собственных функций.
 |
|||
 |
|||


 |
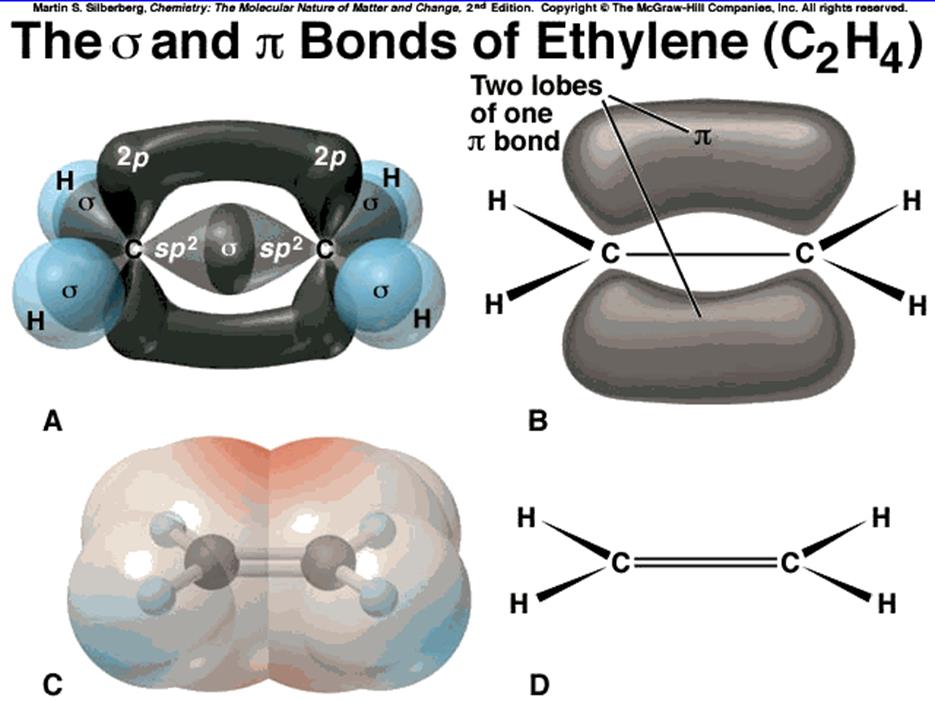
Алканы – международное название.
Предельные (насыщенные) углеводороды – русское название, отражающее неспособность вступать в реакции присоединения.
Парафины – название, отражающее малую химическую активность (parum affinis – (лат.) малое сродство).
![]()
 |
![]() учитывая, что Mядра>>mе можно сначала определить энергию системы электронов
при неподвижных ядрах Uе(R)
учитывая, что Mядра>>mе можно сначала определить энергию системы электронов
при неподвижных ядрах Uе(R)
![]() затем энергию движения ядер, при заданном электронном состоянии
затем энергию движения ядер, при заданном электронном состоянии
Задача о движении двух ядер в поле Uе(R), ( центрально-симметричное поле - энергия электронного терма) сводится к задаче одномерного движения частицы с приведенной массой М в эффективном поле, равном сумме Uк(R) и центробежной энергии
![]() рассматриваем только синглетные термы (полный спин S = 0).
рассматриваем только синглетные термы (полный спин S = 0).
![]() введем
введем![]() - полный момент молекулы,
включающий орбитальный момент электронов
- полный момент молекулы,
включающий орбитальный момент электронов ![]() и момент
вращения ядер.
и момент
вращения ядер.
![]() энергия орбитального движения электронов, определяемая
энергия орбитального движения электронов, определяемая ![]() , входит в энергию электронного терма
, входит в энергию электронного терма
Оператор центробежной энергии ядер:
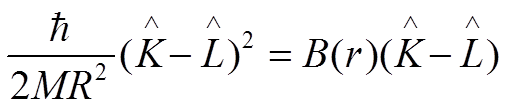 .
.
Усредняя его при заданном R по электронному состоянию, получим значение эффективной потенциальной энергии:
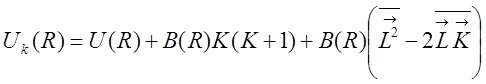 ,
,
![]()
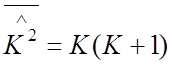 .
.
![]() , где
, где ![]() -
единичный вектор в направлении оси молекулы.
-
единичный вектор в направлении оси молекулы.
У
системы из двух точечных частиц (ядер) момент количества движения направлен
перпендикулярно оси молекулы, 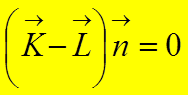 .
.
Следовательно:
![]()
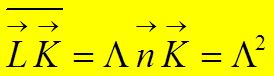
Тогда: 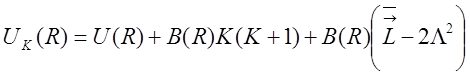 .
.
Последнее слагаемое может быть включено в U(R).
Таким образом, для потенциальной энергии окончательно имеем:
![]() , где К
, где К ![]()
Решение одномерного уравнения Шредингера для потенциала UK(R) рассмотрим в приближении малого смещения относительно положения равновесия R0, в котором U(R) имеет минимум. Тогда
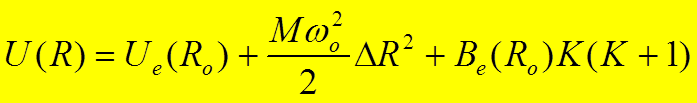 ,
,
где ![]() -
частота колебаний молекулы;
-
частота колебаний молекулы;
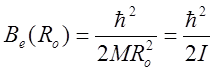 -
ротационная постоянная,
-
ротационная постоянная,
где ![]() - момент инерции молекулы.
- момент инерции молекулы.
Решение уравнения Шредингера для такого потенциала известно:
![]() , где
, где ![]() = 0,1,2...
= 0,1,2...
Энергетические уровни складываются из трех независимых частей:
W = We + WK + ![]() ,
,
· We - отрицательная электронная энергия, определяющая энергию связи молекулы, включая электростатическое взаимодействие ядер.
· WK = BeK(K+1)
при K > ![]() - положительная
энергия ротатора;
- положительная
энергия ротатора;
· ![]() - положительная
колебательная энергия.
- положительная
колебательная энергия.
Поскольку
![]() , а
, а ![]() , то
, то
We
: WK : ![]() = 1 :
= 1 : 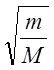 :
: ![]()
Молекулярные термы с отличным от нуля спином S.
Возможны два случая:
(а)
- энергия спин-орбитального взаимодействия WSL велика по сравнению
с разностью между двумя вращательными уровнями ![]() ,
,
(б)
- WSL мала по сравнению с ![]() .
.
Энергия в случае (а):
![]() ,
,
где
J - полный момент молекулы, включающий орбитальный и спиновый моменты
электронов и момент вращения ядер (![]() ).
). 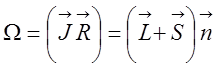 - проекция момента на ось молекулы.
- проекция момента на ось молекулы.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.