Свободно-связанные и связанно-свободные переходы
 Если начальное
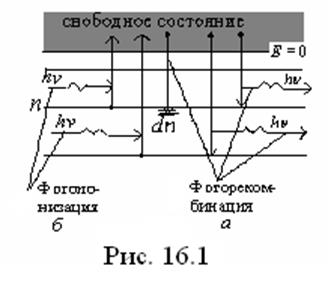
состояние электрона является свободным, а конечное – связанным (рис 16.1а),
говорят о фоторекомбинации в случае присоединения электрона к иону с
образованием атома или о фотозахвате (фотоприлипании) в случае
при-соединения электрона к атому (молекуле) с образованием отрицательного иона.
Если свободным является конечное состояние, а начальное – связанным (рис 16.1б),
говорят о фотоионизации атома или фотоотрыве электрона от отрицательного
иона.
Если начальное
состояние электрона является свободным, а конечное – связанным (рис 16.1а),
говорят о фоторекомбинации в случае присоединения электрона к иону с
образованием атома или о фотозахвате (фотоприлипании) в случае
при-соединения электрона к атому (молекуле) с образованием отрицательного иона.
Если свободным является конечное состояние, а начальное – связанным (рис 16.1б),
говорят о фотоионизации атома или фотоотрыве электрона от отрицательного
иона.
Рассмотрим захват свободного электрона водородоподобным ионом с излучением кванта и образованием водородоподобного атома.
В классической механике
переход от свободных состояний электрона к связанным является непрерывным. Строго
движение можно считать квазиклассическим лишь для высоких электронных уровней,
когда уровни энергии располагаются практически непрерывно. В этом случае
энергия, излучаемая при захвате ![]() электронов, движущихся
со скоростью u ионами
электронов, движущихся
со скоростью u ионами ![]() (т.е. энергия излучения ед. объема в ед.
времени) на группу уровней
(т.е. энергия излучения ед. объема в ед.
времени) на группу уровней ![]() есть
есть
![]() ,
где
,
где ![]() - плотность ионов (16.1).
- плотность ионов (16.1).
В условиях ЛТР излучаемая энергия
должна равняться энергии, поглощаемой при рассеянии ![]() электронов
на
электронов
на ![]() ионах частоты
ионах частоты ![]() (см. (15.26)):
(см. (15.26)):
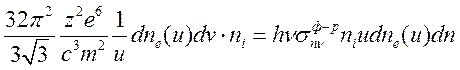 (16.2)
(16.2)
Откуда
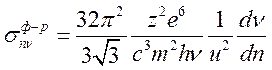 (16.3)
(16.3)
Теперь нам необходимо
установить связь между интервалом излучаемых частот ![]() и
интервалом
и
интервалом ![]() , на которой захватывается электрон.
Рассмотрим электрон, который двигался с некоторой заданной скоростью
, на которой захватывается электрон.
Рассмотрим электрон, который двигался с некоторой заданной скоростью ![]() и был захвачен ионом на уровень
и был захвачен ионом на уровень ![]() с энергией
с энергией ![]() и при
этом излучился квант энергии
и при
этом излучился квант энергии ![]() . Из закона сохранения
энергии имеем
. Из закона сохранения
энергии имеем
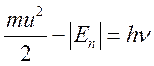 (16.4)
(16.4)
Аналитическое выражение
для ![]() есть только для водородоподобного атома
(иона). Энергетические уровни водородоподобного атома
есть только для водородоподобного атома
(иона). Энергетические уровни водородоподобного атома ![]() характеризуются
главным квантовым числом
характеризуются
главным квантовым числом ![]() , пробегающим значения
от 1 до ¥
, пробегающим значения
от 1 до ¥
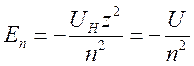 ;
; 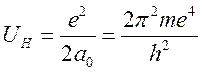 (
(![]() боровский
радиус,
боровский
радиус, ![]() потенциал ионизации атома водорода,
потенциал ионизации атома водорода, ![]() зарядовое число);
зарядовое число); ![]() -
абсолютная величина энергии основного состояния, т.е. потенциал ионизации.
Подставляя значение
-
абсолютная величина энергии основного состояния, т.е. потенциал ионизации.
Подставляя значение![]() в (16.4) и дифференцируя (при
в (16.4) и дифференцируя (при ![]() ) получим
) получим 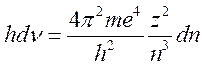 , откуда
, откуда
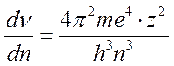 (16.5).
(16.5).
После подстановки (16.5) в (16.3)
найдем сечение рекомбинационного излучения, связанное с захватом электрона на
уровень ![]() и излучением квантов частоты
и излучением квантов частоты ![]() .
.
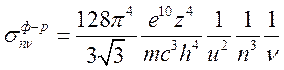 (16.6).
(16.6).
Перейдем к рассмотрению
процессов, связанных с поглощением атомом излучения частоты ![]() и отрывом связанного электрона,
находящегося в атоме на уровне
и отрывом связанного электрона,
находящегося в атоме на уровне ![]() , с образованием иона и
свободного электрона. Как мы уже говорили, этот процесс носит название
фотоионизации. Для нахождения сечения фотоионизации
, с образованием иона и
свободного электрона. Как мы уже говорили, этот процесс носит название
фотоионизации. Для нахождения сечения фотоионизации ![]() и
коэффициента поглощения связанно-свободных переходов
и
коэффициента поглощения связанно-свободных переходов
![]() (16.7)
воспользуемся принципом детального равновесия.
(16.7)
воспользуемся принципом детального равновесия.
Вновь обратимся к формуле (16.1), где выражение в левой части есть, по сути дела, лучеиспускательная способность газа, связанная с захватом электронов на n-ый уровень и
![]() (16.8)
(16.8)
Используя закон Кирхгофа (15.29) с учетом (16.7) из (16.8) имеем:
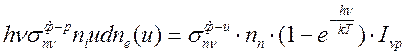 (16.9),
(16.9),
определяющую связь между сечением
рекомбинационного излучения ![]() и сечением
фотоинизационного поглощения
и сечением
фотоинизационного поглощения ![]() . Прежде чем
преобразовать выражение (16.9) выпишем необходимые соотношения:
. Прежде чем
преобразовать выражение (16.9) выпишем необходимые соотношения:
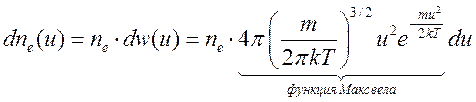 (16.9а);
(16.9а);
из (16.4) для фиксированного уровня
![]() ,
а
,
а 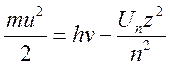 (16.9b);
(16.9b);
населенность n-го уровня
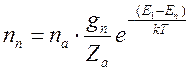 (16.9с),
(16.9с),
где для водородоподобного атома ![]() , а статистическая сумма атома
, а статистическая сумма атома
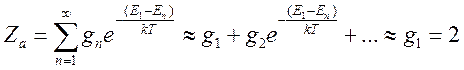 ;
;
уравнение Саха, связывающее концентрации электронов, ионов и атомов:
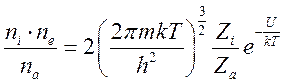
![]() (16.9d).
(16.9d).
С учетом (16.9а), (16.9b),(16.9c),(16.9d) формула (16.9) сильно упрощается
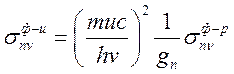 (16.10).
(16.10).
Подставляя в (16.10) выражение ![]() из (16.6) находим искомое сечение фотоионизации
из (16.6) находим искомое сечение фотоионизации
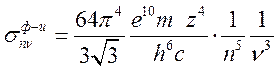 (16.11)
(16.11)
В формулу (16.11) удобно
ввести пороговую (минимальную) частоту фотона, начиная с которой он может
вырвать электрон с уровня ![]() , которая определяется
из выражения (16.9b) если положить
скорость равной нулю
, которая определяется
из выражения (16.9b) если положить
скорость равной нулю
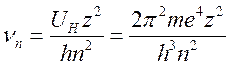 (16.12),
(16.12),
тогда (16.11) с учетом (16.12) перепишется
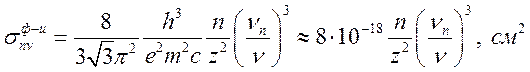 (16.13)
(16.13)
Выражение (16.13) также
называется формулой Крамерса. Характерной особенностью сечения ![]() является быстрое убывание (как
является быстрое убывание (как ![]() ) с ростом квантового числа и обратная
кубическая зависимость от частоты.
) с ростом квантового числа и обратная
кубическая зависимость от частоты.
Более строгое квантовомеханическое рассмотрение фотоионизации водородоподобных атомов приводит к появлению в формуле (16.11) ((6.13)) поправочного множителя – фактора Гаунта [4]
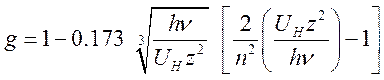 , (16.14)
, (16.14)
который в большинстве практически интересных случаев близок к единице.
Для сложных атомов,
применения формулы (16.11) для основного состояния может давать значительную
ошибку, особенно сильное отличие в ![]() у существенно
неводородоподобных атомов, как, например, у щелочных металлов.
у существенно
неводородоподобных атомов, как, например, у щелочных металлов.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.