Свободно-связанные и связанно-свободные переходы, страница 2

Теперь несколько слов об излучении, связанном с фотозахватом электронов нейтральными атомами с образованием отрицательных ионов и, соответственно поглощением излучения при фотоотрыве электрона от отрицательного иона. Особое значение имеют отрицательные ионы водорода , играющие важную роль в лучистом переносе в звездных атмосферах и отрицательные ионы кислорода , дающие существенный вклад в непрерывный спектр поглощения воздуха. Нахождение соответствующих сечений фотозахвата и фотоотрыва, является гораздо более сложной задачей чем определение сечений фоторекомбинации и фотоионизации, т.к. электрон в отрицательном ионе находится под действием короткодействующего поля атома и такая система не может рассматриваться классически даже приближенно. Квантомеханические расчеты для каждого конкретного отрицательного иона не всегда дают удовлетворительные результаты в сравнении с экспериментом. Анализ экспериментальных значений фотоотрыва показывает, что значения их лежат в районе  см², т.е. в той же области, где и сечения фотоионизации, поэтому оценку роли всех этих процессов в переносе излучения необходимо проводить совместно.

Коэффициент поглощения плазмы в непрерывном спектре

Полный коэффициент непрерывного поглощения складывается из суммы коэффициента тормозного поглощения свободными электронами в полях ионов и коэффициента поглощения при фотоионизации

                                                                                      (16.15),

где  определяется выражением (15.30)

,

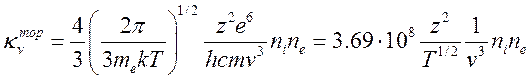а коэффициент поглощения при фотоионизации есть

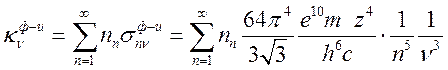                                                  (16.16).

Преобразуем , выразив произведение  через  с помощью уравнения Саха (16.9d):

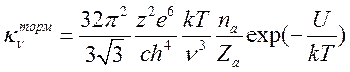                                                                (16.17).

Рассмотрим более подробно выражение (16.16) для коэффициента поглощения при фотоионизации. Видно, что если энергия кванта превышает энергию связи электрона в основном состоянии атома, т.е. потенциал ионизации , то в поглощении участвуют все атомы. В поглощении очень малых квантов  участвуют только высоковозбужденные атомы .

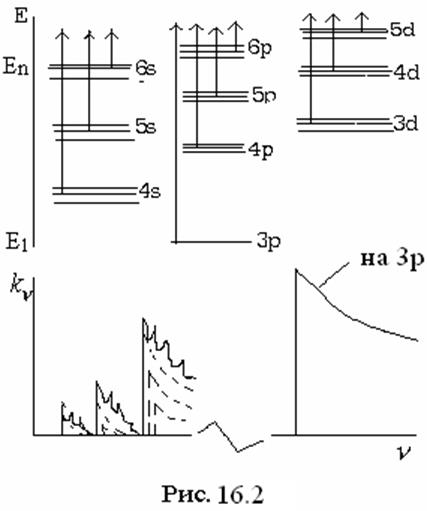Кривая поглощения, в зависимости от частоты имеет характер «частокола». На рис. 16.2. представлена условные схема терма атома аргона и вид . Как только энергия кванта  возрастая, достигает энергии связи электрона в каком-нибудь состоянии , то атомы возбужденные до этого уровня, включаются в поглощение и  возрастает скачком. Затем, вплоть до включения следующего уровня,  уменьшается как . Полный коэффициент поглощения получается путем суммирования всех зубцов на данный частоте. Преобразуем выражение (16.16), считая атомы, участвующие в поглощении водородоподобными. Тогда 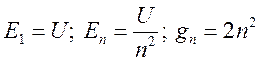 и населенность уровня , определяемая формулой (16.9с) запишется

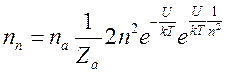                                                                                 (16.18).

После подстановки (16.18) в (16.16) получим

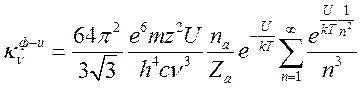                                                              (16.19).

Складывая (16.17) и (16.19), получаем окончательное выражение для коэффициента поглощения в непрерывном спектре

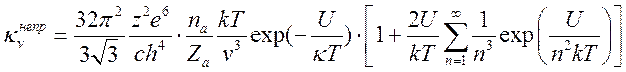                        (16.20).

Интегральные формулы

Из (16.20) видно, что при больших  члены суммы, стоящие в квадратных скобках представляют быстросходящий ряд, что физически соответствует тому, что при больших квантовых числах сечения отдельных процессов фотоионизации лежат достаточно плотно и, перекрываясь, дают сравнительно гладкую кривую. В этом случае суммирование можно приближенно заменить интегрированием, при этом нижним пределом суммы должен быть номер уровня , начиная с которого можно не учитывать фотоионизацию индивидуально и вычислить сумму приближенно. Уровни выше  должны лежать плотно. В силу сказанного

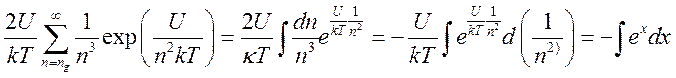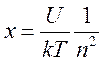,       (16.21)

Теперь установим границы интегрирования в (16.21). Мы должны каждый раз вычислять интеграл от некоторой минимальной частоты, соответствующей поглощению на уровень с энергией  и до границы со сплошным спектром , причем согласно (16.12) энергия, соответствующая этой частоте есть 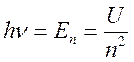 и интеграл в правой части (16.21) есть

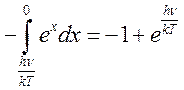                                                                    (16.22)

 и коэффициент поглощения непрерывного спектра представляется

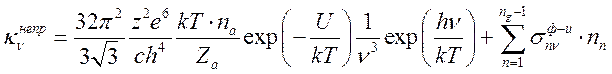                          (16.23).

Здесь первое слагаемое есть результат замены в (16.20) суммирования интегрированием, а второе слагаемое есть коэффициент поглощения, связанный с фотоионизацией группы уровней, учитываемых индивидуально. На практике это основной уровень и несколько близ лежащих к нему уровней, определяемых из вида конкретного терма атома.

Формула (16.23) верна для  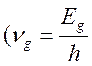, E_g ‘энергия граничного уровня). При  в последней экспоненте вместо  следует подставить , т.к. интегрирование ведется при этом до  ( -  номер уровня, начиная с которого фотоионизация учитывается интегрально).

Сложные атомы

Формула (16.23) справедлива строго (с учетом квантовомеханических поправок – факторов Гаунта) лишь для водородоподобных атомов. Берджес и Ситон получили выражение для сечения фотоионизации произвольного атома и иона с помощью метода квантового дефекта. Метод квантового дефекта приближенно учитывает отличие волновой функции данного состояния сложного атома от водородоподобного. Квантовый дефект , равный разности квантового числа  данного уровня сложного атома с энергией  и эффективного квантового числа , полученного для той же энергии  из формулы для водородоподобного атома , позволяет использовать для расчетов комбинации водородных волновых функций.

Биберман и Норман, используя сечение фотоионизации Бирджеса и Ситона [5,6], получили интегральные формулы для коэффициента поглощения, отличающиеся от (16.23) поправочным множителем  - т.н. кси-фактором.

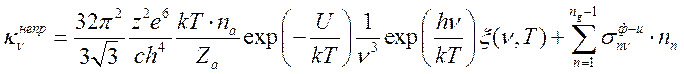                     (16.24).

 сравнительно слабо зависит от температуры и для таких газов, как углерод, азот, кислород, гелий, неон, криптон, ксенон, литий, магний, ртуть является функцией только частоты . В настоящее время -факторы рассчитаны для большинства важных атомов и ионов.