Реакция системы на произвольную функцию времени [1, c.182].
Пусть для системы с
передаточной функцией ![]() известна реакция на единичную
импульсную функцию
известна реакция на единичную
импульсную функцию ![]() . Эта реакция называется функцией
веса. Она связана с передаточной функцией преобразованием Лапласа:
. Эта реакция называется функцией
веса. Она связана с передаточной функцией преобразованием Лапласа:
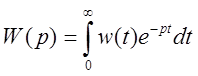
Если на вход
системы поступает функция времени ![]() , изображение которой
, изображение которой ![]() , то изображение выходной величины имеет
вид произведения:
, то изображение выходной величины имеет
вид произведения:
![]() .
.
Функция времени на выходе, согласно теореме свёртывания, имеет вид:
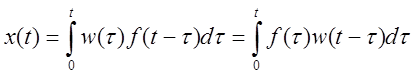 .
.
Здесь ![]() ,
, ![]() –
оригиналы функций
–
оригиналы функций ![]() ,
, ![]() . То
есть
. То
есть ![]() – функция веса, а интеграл – интеграл
Дюамеля.
– функция веса, а интеграл – интеграл
Дюамеля.
Уравнение с переменными коэффициентами [4, c.502].
С помощью преобразования Лапласа можно интегрировать некоторые виды дифференциальных уравнений с переменными коэффициентами следующего вида:
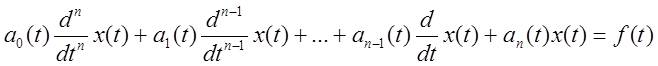 .
.
Коэффициенты ![]() – полиномы от t.
Преобразование Лапласа:
– полиномы от t.
Преобразование Лапласа:
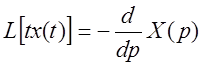 ,
, 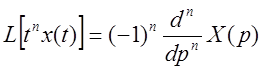 ,
, 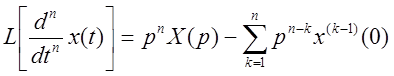 ,
, 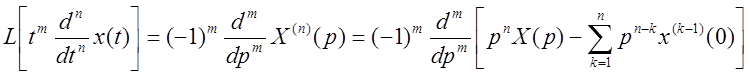 .
.
В результате
имеем обыкновенное дифференциальное уравнение относительно изображения ![]() . Порядок равен наивысшей степени t в исходном уравнении. Преобразованное уравнение
оказывается проще исходного, хотя и остаётся уравнением с переменными
коэффициентами.
. Порядок равен наивысшей степени t в исходном уравнении. Преобразованное уравнение
оказывается проще исходного, хотя и остаётся уравнением с переменными
коэффициентами.
Пример уравнения [4, с.504].
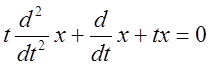 .
.
Начальные условия: ![]() ,
, ![]() .
Уравнение относительно изображения:
.
Уравнение относительно изображения:
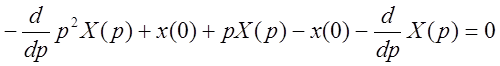 ,
, 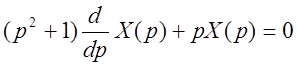 .
.
Разделение переменных даёт:
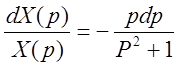 ,
, 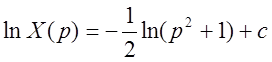 ,
, 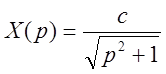 .
.
По теореме о начальном значении оригинала:
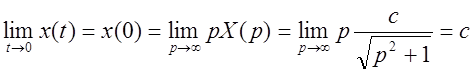 . Следовательно,
. Следовательно, ![]() .
.
Определение оригинала
осуществляется по таблице: 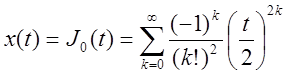 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.