Расчет состава низкотемпературной плазмы

Лекция № 8

Расчет состава низкотемпературной плазмы

В общем случае развитый выше подход к плазме применен быть не может, так как при наличии кулоновского взаимодействия энергетические степени свободы нельзя считать независимыми и статистическая сумма системы не может быть представлена в виде произведения статистических сумм отдельных элементов. Это можно сделать для слабонеидеальной плазмы в приближении слабого взаимодействия ее составляющих между собой. При этом полная сумма по состояниям распадается на суммы по компонентам, которые, в свою очередь, могут быть приближенно сведены к статистическим суммам отдельных частиц.

Для простоты рассмотрим газ, состоящий из атомов одного элемента. Реакцию ионизации в символьном виде можно записать:

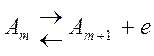,   ,                                       (8.1),

где  ,будет соответствовать атому,  - однократно ионизованному атому (первому иону),  - двукратно ионизованному атому (второму иону) и т. д. Средняя удельная (на единицу объема) внутренняя энергия газа будет:

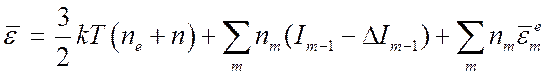                                 (8.2),

здесь  - число электронов, исходных атомов,  - тых ионов ( соответствует атому) в единице объема соответственно;  - энергия электронного возбуждения  - кратного иона (включая и атом);  - потенциалы последовательных ионизаций ( - потенциал ионизации атома,  - потенциал ионизации однократно ионизованного иона,  - потенциал ионизации двукратно ионизованного иона и т.д., ); - снижение потенциала ионизации, которое будет рассмотрено ниже.

Введем безразмерные концентрации ; , тогда выражение для внутренней энергии (8.2) можно записать как

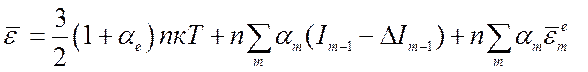                           (8.3).

Число атомов, ионов и электронов связаны между собой условием сохранения числа частиц

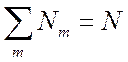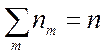     ( или 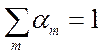)                                               (8.4)

где N – число исходных атомов и сохранением числа зарядов

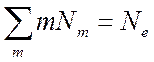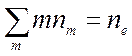     ( или 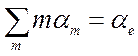)                                   (8.5).

Связь между концентрациями атомов, ионов и электронов определяется уравнением (7,21), где для реакции (8.1)

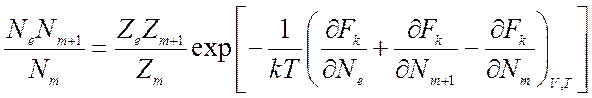                    (8.6).

Здесь - свободная энергия, связанная с кулоновским взаимодействием,  - статистическая сумма иона (атома) по электронным состояниям,  - статистическая сумма свободного электрона. Поступательные суммы обоих ионов сократились, так как массы ионов практически мало отличаются (на величину ) друг от друга.

Выделим в статистической сумме 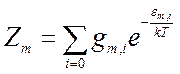 множитель, соответствующий  энергии основного состояния

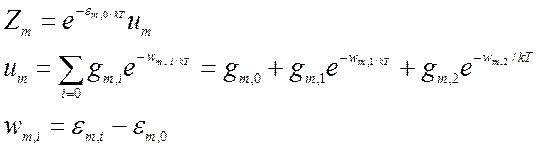                                 (8.7),

где  - представляет собой энергию возбуждения -го иона в -том состоянии, причем  - потенциал ионизации иона кратности m,  статистические веса энергетических уровней.

Статистическая сумма свободного электрона состоит из произведения поступательной суммы на статистический вес, равной 2 в соответствии с двумя возможными ориентациями спина, то есть

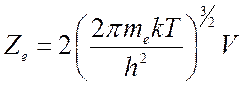                                    (8.8).

Введем также обозначение

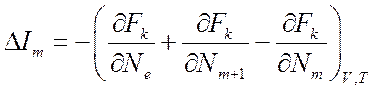                                                                    (8.9).

И в итоге из (8.6) с учетом (8.7) - (8.9) следует уравнение ионизационного равновесия (уравнение Саха)

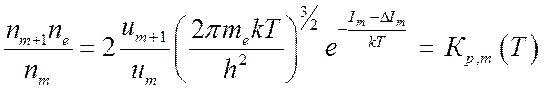                                 (8.10).

Переходя в левой части уравнения (8.10) к концентрациям  и  получим

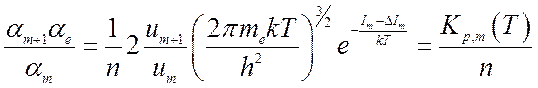                                  (8.11).

Теперь займемся определением величина . Условием слабой неидеальности плазмы есть малость кулоновской энергии по сравнению с тепловой

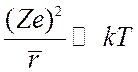                                                   (8.12),

где Z - среднее зарядовое число  - среднее расстояние между заряженными частицами. Это условие обычно выполняется при давлении до сотен атмосфер. Выполнение условия (8.12) позволяет для расчета потенциала в плазме использовать распределение Больцмана. Потенциал, создаваемый частицей с зарядом  на расстоянии r от нее находится из решения линеаризованного уравнения Пуассона для самосогласованного поля и имеет вид

                                                                                                    (8.13),

где - дебаевский радиус экранирования:

                                                                                              (8.14).

Поскольку статистическое рассмотрение Дебая-Хюккеля справедливо, если , (в сфере Дебая должно находится достаточно большое количество частиц), то из (8.13) после разложения экспоненты по малому показателю находим:

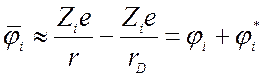                                                                                    (8.15).

Здесь первый член есть потенциал, создаваемый самим ионом  в точке , а второй - есть потенциал, создаваемый окружающими зарядами в месте, где находится ион.

Как известно, взаимная  энергия системы  точечных зарядов есть 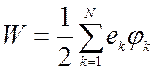, где  есть потенциал поля в точке, занимаемой зарядом . Тогда в рассматриваемом случае кулоновская энергия в объеме  есть

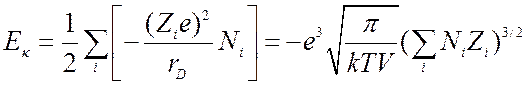                                                  (8.16).

          Из выражения (7.14) имеем 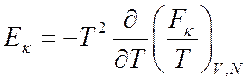 , откуда после интегрирования следует

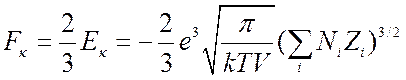
                                                                       (8.17).

Поправка к давлению

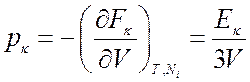                                                                                      (8.18).

Для  . В среднем между частицами действуют силы притяжения, так как каждый ион окружает себя преимущественно зарядами противоположного знака. Поэтому кулоновская энергия и давление  отрицательны.

 Кулоновское взаимодействие уменьшает энергию и давление плазмы и, кроме того, сдвигает ионизационное равновесие в сторону более высокой ионизации. Формально это связано с величиной , уменьшающей энергию ионизации (см. (8.10)).Дифференцируя (8.17), получаем

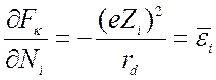                                                  (8.19),

так что формула (8.9) эквивалентна выражению

                                                                                           (8.20).

В частности, для ионизации атома

                                                                                             (8.21).

          Рассмотрим физический смысл .