Для наиболее интересного, с точки зрения задач газовой динамики, диапазона температур 6000 – 20000 K, существенна только первая ионизация, а вторая минимальна, поскольку потенциал второй ионизации значительно (от 2 до 10 раз) превышает первый.
Тогда для однократной ионизации из системы (8.11) остается только одно уравнение:
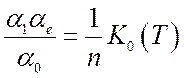 (8.24).
(8.24).
Поскольку ![]() ,
, ![]() то из (8.24) получаем
то из (8.24) получаем
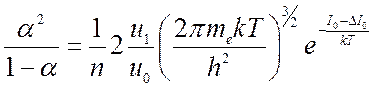
![]() (8.25).
(8.25).
Уравнение
состояния для ионизованного газа без учета ![]()
![]() есть:
есть:
![]() (8.26).
(8.26).
В случае однократного ионизованного газа
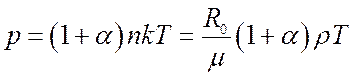 (8.27),
(8.27),
откуда 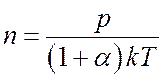 и
выражение (8.25) можно переписать через давление:
и
выражение (8.25) можно переписать через давление:
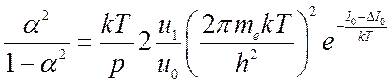 (8.28).
(8.28).
Отметим, что
для расчетов, не требующих высокой точности, вкладом ![]() во
внутреннюю энергию ((8.2),(8.3)) можно пренебречь, тогда как в уравнениях
(8.10) учет его необходим, поскольку он входит в показатель экспоненты.
во
внутреннюю энергию ((8.2),(8.3)) можно пренебречь, тогда как в уравнениях
(8.10) учет его необходим, поскольку он входит в показатель экспоненты.
Приложение.
Основные термодинамические соотношения в случае однократной ионизации.
Для
практически наиболее интересного диапазона температур до ![]() с большой степенью точности возбуждение
атомов и ионов можно не учитывать и считать, что все атомы и ионы находятся в
основном состоянии. В этом случае статистическая сумма по состояниям для них
может быть заменена статистическими весами основных состояний, то есть
с большой степенью точности возбуждение
атомов и ионов можно не учитывать и считать, что все атомы и ионы находятся в
основном состоянии. В этом случае статистическая сумма по состояниям для них
может быть заменена статистическими весами основных состояний, то есть ![]() для атома;
для атома; ![]() для
иона. Обозначим потенциал ионизации атома через I,
тогда удельные на единицу объема величины есть:
для
иона. Обозначим потенциал ионизации атома через I,
тогда удельные на единицу объема величины есть:
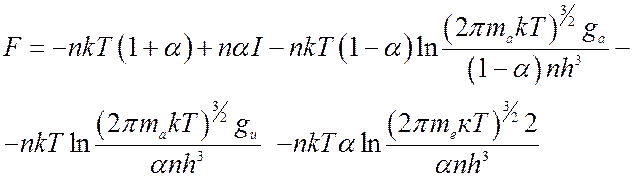 (8.29);
(8.29);
Внутренняя энергия
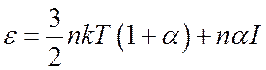 (8.30);
(8.30);
Энтропия
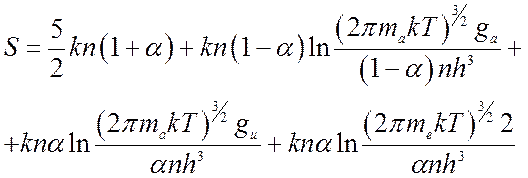 (8.31);
(8.31);
Энтальпия
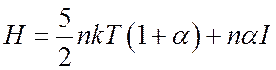 (8.32).
(8.32).
Уравнение Саха
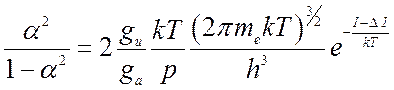 (8.33),
(8.33),
где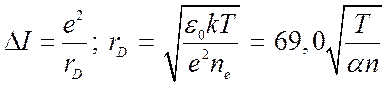 [м].
[м].
Определим теплоемкости ![]() и
и ![]() . Из
(8.32) получим
. Из
(8.32) получим
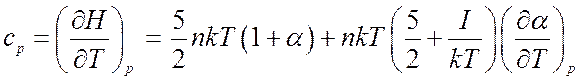 ,
, 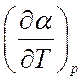 находится путем дифференцирования
уравнения (8.33), которое удобно вначале прологарифмировать (левую и правую
части), тогда
находится путем дифференцирования
уравнения (8.33), которое удобно вначале прологарифмировать (левую и правую
части), тогда
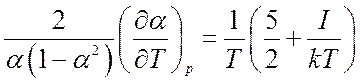 откуда
откуда
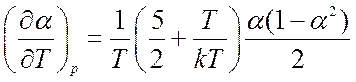 и
и
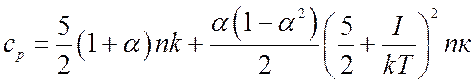 (8.34).
(8.34).
Теплоемкость ![]() согласно (8.30) есть
согласно (8.30) есть
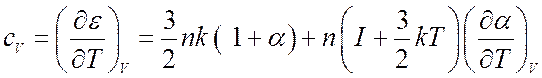 .
Определяя производную
.
Определяя производную 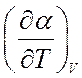 аналогичным образом из (8.33),
окончательно будем иметь
аналогичным образом из (8.33),
окончательно будем иметь
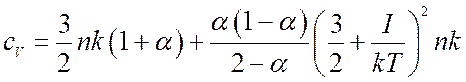 (8.35).
(8.35).
Отношение удельных теплоемкостей
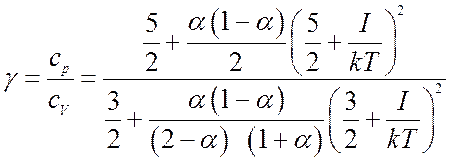 (8.36).
(8.36).
Отметим, что выражение ![]() известное
как адиабата Пуасона в случае реакции ионизации будет справедливо только для
полностью ионизованной плазмы (
известное
как адиабата Пуасона в случае реакции ионизации будет справедливо только для
полностью ионизованной плазмы (![]() ).
).
Определим адиабатическую скорость
звука 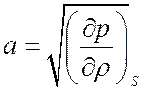 . Условие постоянства энтропии запишем в
виде
. Условие постоянства энтропии запишем в
виде ![]() , причем здесь вместо энтропии
, причем здесь вместо энтропии ![]() , отнесенной к единице объема удобнее взять
энтропию
, отнесенной к единице объема удобнее взять
энтропию ![]() , отнесенную к единице массы, очевидно
, отнесенную к единице массы, очевидно ![]() и, используя выражение для энтропии (8.31),
получим выражение для скорости звука
и, используя выражение для энтропии (8.31),
получим выражение для скорости звука
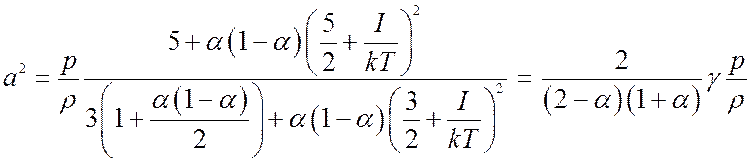 (8.37),
(8.37),
где ![]() определяется выражением (8.36).
определяется выражением (8.36).
Все формулы (8.29) – (8.37)
превращаются в обычные термодинамические соотношения для одноатомного
идеального газа, если положить ![]() (газ не ионизован), или
(газ не ионизован), или
![]() (газ полностью ионизован).
(газ полностью ионизован).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.