Распространении фронта горения в газе, способном к химической реакции

Лекция № 3

Распространении фронта горения в газе, способном к химической

реакции.

Пусть мы имеем трубу, заполненную газообразной горючей смесью (рис. 3.1а). У левого торца трубы происходит поджиг и воспламенение смеси. 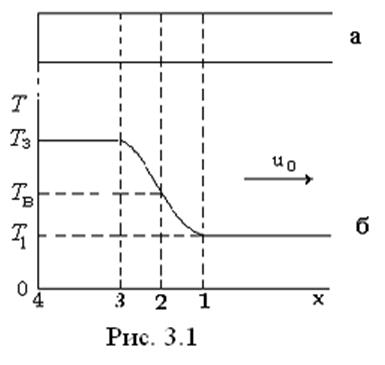В схематизированном и упрощенном виде последовательность физических явлений в этом процессе можно условно разбить на несколько  стадий: в зоне (3) осуществляется поджиг и происходит горение смеси; в области (2) за счет теплопроводности происходит прогрев горючей смеси от начальной температуры Т₁ до температуры воспламенения Т_в, после чего там происходит воспламенение и далее она сливается с областью (3). Таким образом вся картина стационарным образом с постоянной скоростью перемещается по каналу. На рис. 3.1б представлен условный профиль температуры, соответствующей описанному выше процессу. В области  2-3 идет  химическая реакция с выделением тепла, а после завершения реакции образуется однородная область 3-4 продуктов горения, имеющих высокую температуру Т₃. Для решения задачи в качестве исходного уравнения будем рассматривать уравнение энергии в форме первого начала термодинамики

.

Здесь  количество тепла и внутренняя энергия на единицу массы соответственно, 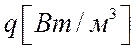 - удельная мощность тепловых источников,  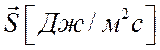 - поток тепла. С учетом того, что , где  - энтальпия на единицу массы, уравнение энергии запишется:

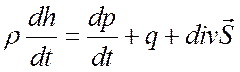,                                                                                          (3.1)

где 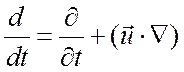 - полная (субстанциональная) производная по времени. В случае, когда лучистым теплообменом можно пренебречь , где k – коэффициент теплопроводности.

            Задачу мы будем рассматривать в стационарном одномерном приближении, газ будем считать идеальным  . Поскольку скорость  распространения  пламени много меньше скорости звука, то по каналу успевает выровняться давление и можно считать, что процесс идет при , тогда уравнение энергии запишется

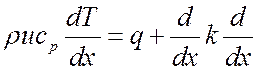                                                                                        (3.2).

Уравнение (3.2) необходимо дополнить  стационарным уравнением неразрывности 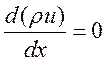 откуда в системе координат, связанной с фронтом распространения пламени имеем

                                                                                                     (3.3).

В области 1-2 выделение тепла не происходит  и из (3.2) с учетом (3.3) имеем:

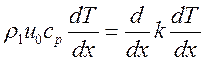                                                                                                (3.4),

откуда после интегрирования от состояния (1) 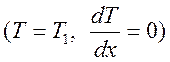до состояния (2) () получим

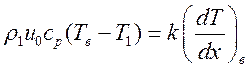                                                                                         (3.5).

В области (2-3), где происходит воспламенение, и горение смеси уравнение энергии есть:

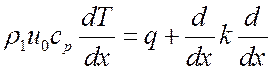                                                                                     (3.6),

где q - тепловыделение за счет химической реакции. Поскольку в областях (1) и (3) Т = соnst то в переходной области (2) профиль температуры будет иметь (по крайней мере) точку перегиба, где . Полагая, что это происходит вблизи Т = Т_в и коэффициент теплопроводности там постоянен, пренебрежем в правой части уравнения (3.6) членом 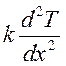 по сравнению с q, тогда

r₁и₀с_p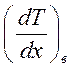 =q                                                                                           (3.7).

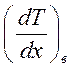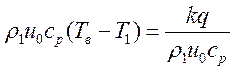В силу непрерывности, на линии (2) (рис. 1б) решения уравнений (3.5) и (3.7) должны «сшиваться». Выражая  из (3.7) и подставляя в (3.5) получим , откуда скорость распространения волны горения есть:

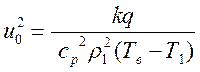                                                                                     (3.8).

Для метано-воздушных смесей с ;  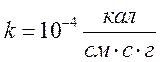;  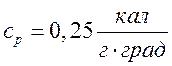(1 кал = 4.1868 Дж) и r₁ = 10^-3 г/см³,  для Т_в – Т₁ = 1000 К получаем . Экспериментально измеренные значения для этих условий есть 10 – 25 см/с. Подчеркнем, что здесь речь идет о спокойном, ламинарном режиме горения.  Если среда перед фронтом горения турбулизована, как это бывает при горении в потоках, скорость волны горения резко возрастает, примерно на порядок, по сравнению с ламинарным режимом.

Ударные волны в реагирующем газе. Детонация.

Быстрое изменение состояния газа при переходе через фронт УВ, в частности повышение его температуры может стать причиной развития тех или иных физико-химических превращений среды (химических реакций, диссоциации, ионизации и т.д.). В процессе протекания этих неравновесных процессов затрачивается или наоборот, пополняется тепловая энергия частиц газа, что обычно учитывается путем введения в уравнение энергии соответствующей величины ± q, выражающей тепловой эффект реакции. Не рассматривая кинетических процессов в самой УВ можно определить общую тенденцию влияния теплового эффекта реакции на изменение газодинамических параметров при переходе через УВ, используя, как и ранее, законы сохранения.

Рассмотрим распространение УВ по неподвижному газу. Выпишем законы сохранения на разрыве

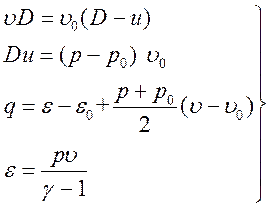                                                                          (3.9),

последнее уравнение в (3.9) есть калорическое уравнение состояния идеального газа. Дифференцируя соотношения (3.9) при постоянных начальных параметрах и скорости УВ получим:

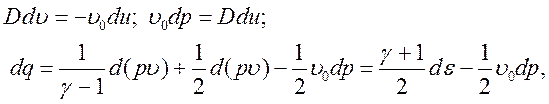
откуда следует

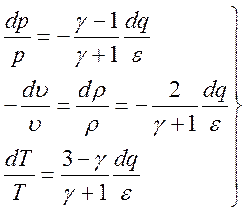                                                                              (3.10).