Из (3.10) видно, что в случае dq > 0, т.е. для реакции с выделением тепла, растет только температура, а давление и плотность падают; в случае dq < 0 эффект обратный. Интересно отметить, что относительное изменение давления в 4-5 раз меньше соответствующих вариаций плотности и температуры.
Отметим также, что стационарное распространение УВ возможно лишь при непрерывном пополнении ее энергии, которая расходуется на нагрев среды и на увеличение кинетической энергии газа за фронтом. Наиболее типичным энергетическим источником пополнения энергии УВ является движение в среде какого-либо тела с большой скоростью (снаряд, ракета, поршень и т.п.) в этом случае скорость УВ однозначно определяется скоростью границы «поддерживающей» течение. В среде способной к тепловыделениям при сжатии в УВ, необходимость в поддерживающем источнике может отпасть. Самоподдерживающиеся ударные волны получили название детонационных волн (ДВ).
Поскольку тепловой эффект реакции входит только в уравнение энергии, то условия сохранения массы и импульса имеют тот же вид, что и для идеальной УВ, и для скорости УВ равной скорости детонации сохранится то же выражение:
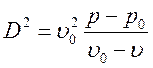 , (3.11),
, (3.11),
а из уравнения энергии следует ударная адиабата
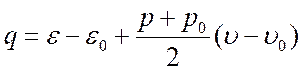 (3.12).
(3.12).
 Прежде всего, отметим, что ударная адиабата детонации должна
качественно отличаться от ударной адиабаты в инертном веществе. Выделение тепла
приводит к смещению кривой конечных состояний по сравнению с адиабатой Пуассона
и с адиабатой ударного перехода без тепловыделения. На диаграмме
Прежде всего, отметим, что ударная адиабата детонации должна
качественно отличаться от ударной адиабаты в инертном веществе. Выделение тепла
приводит к смещению кривой конечных состояний по сравнению с адиабатой Пуассона
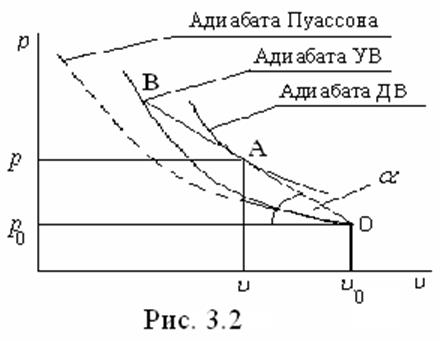
и с адиабатой ударного перехода без тепловыделения. На диаграмме ![]() (рис. 3.2) это будет выглядеть следующим
образом. Проведем из точки О, обозначающей исходное состояние газа, касательную
к ударной адиабате детонационной волны Обозначим точку касания через А.
В точке А по построению
(рис. 3.2) это будет выглядеть следующим
образом. Проведем из точки О, обозначающей исходное состояние газа, касательную
к ударной адиабате детонационной волны Обозначим точку касания через А.
В точке А по построению
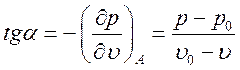 (3.13).
(3.13).
Продифференцируем (3.12) по ![]() (
(![]() –постоянные величины).
–постоянные величины).
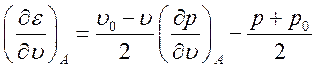 (3.14).
(3.14).
Подставляя 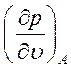 из (3.13) в
(3.14) получим
из (3.13) в
(3.14) получим 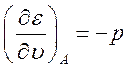 , с
другой стороны для адиабаты Пуассона
, с
другой стороны для адиабаты Пуассона ![]() имеем
имеем 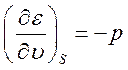 , откуда следует, что
, откуда следует, что
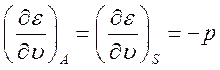 (3.15).
(3.15).
Из калорического уравнения состояния имеем 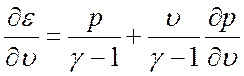 и из
(3.15) получаем
и из
(3.15) получаем
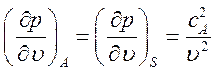 , (3.16)
, (3.16)
где 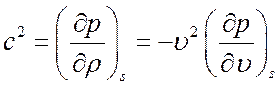 -
скорость звука.
-
скорость звука.
Подставляя в (3.16) значение 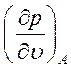 из
(3.13) находим:
из
(3.13) находим:
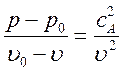 (3.17).
(3.17).
Из законов сохранения (3.9) на ДВ следует:
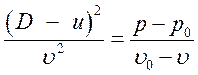 (3.18).
(3.18).
Подставляя (3.18) в (3.17) получаем:
![]() или
или ![]() (3.19)
(3.19)
Этот результат,
полученный Чепменом и Жуге имеет простой физический смысл: в .детонационной
волне, соответствующей переходу ОА, любые малые возмущения распространяются
со скоростью ![]() т.е. со скоростью фронта
ДВ, следовательно не могут догнать его и изменить интенсивность ДВ. Точка А
(Точка Чепмена-Жуге) таким образом описывает особый режим распространения волны
– состояние самоподдерживающейся детонации, поскольку волна разрежения, обычно
возникающая при расширении сгоревших продуктов за ударным фронтом, не может в
этих условиях догнать фронт и соответственно ослабить интенсивность волны.
т.е. со скоростью фронта
ДВ, следовательно не могут догнать его и изменить интенсивность ДВ. Точка А
(Точка Чепмена-Жуге) таким образом описывает особый режим распространения волны
– состояние самоподдерживающейся детонации, поскольку волна разрежения, обычно
возникающая при расширении сгоревших продуктов за ударным фронтом, не может в
этих условиях догнать фронт и соответственно ослабить интенсивность волны.
 Продолжим
прямую ОА до её пересечения с ударной адиабатой газа, построенной в
предположении о том, что горения нет (рис. 3.2).Точка (В) описывает состояние
за фронтом УВ, распространяющегося также со скоростью детонации D, в том же газе но не реагирующем.
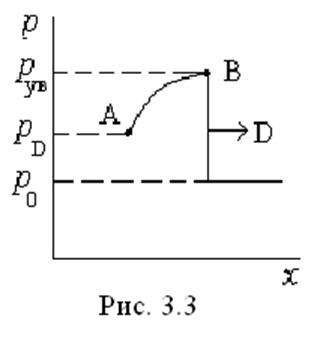
Поскольку характерное время протекания любой химической реакции много больше
времени ударного перехода, можно представить себе упрощенную схему структуры
детонации волны (рис. 3.3): вначале за фронтом УВ достигается состояние, соответствующее
точке В. (реакция не началась), а затем согласно (3.10) по мере
протекания реакции, давление и плотность постепенно умень-шаются и мы переходим
по линии ВА в состояние с завершенной химической реакцией. Определим скорость
детонации по известному тепловому эффекту химической реакции. Из законов
сохранения (3.9) и калорического уравнения состояния в предположении
Продолжим
прямую ОА до её пересечения с ударной адиабатой газа, построенной в
предположении о том, что горения нет (рис. 3.2).Точка (В) описывает состояние
за фронтом УВ, распространяющегося также со скоростью детонации D, в том же газе но не реагирующем.
Поскольку характерное время протекания любой химической реакции много больше
времени ударного перехода, можно представить себе упрощенную схему структуры
детонации волны (рис. 3.3): вначале за фронтом УВ достигается состояние, соответствующее
точке В. (реакция не началась), а затем согласно (3.10) по мере
протекания реакции, давление и плотность постепенно умень-шаются и мы переходим
по линии ВА в состояние с завершенной химической реакцией. Определим скорость
детонации по известному тепловому эффекту химической реакции. Из законов
сохранения (3.9) и калорического уравнения состояния в предположении ![]() (сильной УВ) после несложных выкладок можно
получить
(сильной УВ) после несложных выкладок можно
получить
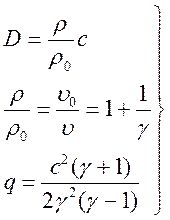 (3.20).
(3.20).
Откуда следует выражение для скорости ударной волны
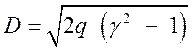 (3.21).
(3.21).
Эксперименты
показывают, что эта приближенная формула не только дает достаточно правильное
представление о величине скорости детонации для большинства детонирующих
газовых смесей, но она оказывается применимой также и для оценки скорости
детонации конденсированных взрывчатых веществ, где для продуктов реакции, находящихся
при давлениях 105 – 106 атм., принимается g = 3. Если в газах величина скорости детонации ~ 2500 – 3000 м/с, то для
конденсированных сред она ~ 7 км/с, что
согласуетcя с экспериментом. Для обычной сильной УВ 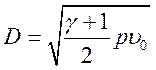 и при больших р может быть очень большой, в то
время как скорость ДВ строго ограничена выражением (3.21).
и при больших р может быть очень большой, в то
время как скорость ДВ строго ограничена выражением (3.21).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.