Практикум по радиоэлектронике. Трансформатор: Методические указания к лабораторной работе № 12, страница 7

Z₁ = r₁+n² ∙ r₂ + j ∙ ω(L_S1+n² ∙ L_S2) + n² ∙ Z_Н = (r₁ + j ∙ ω ∙ L_S1)+

+n²∙(r₂+j∙ω∙L_S2+Z_Н),

где выделенное слагаемое представляет собой сопротивление, которое трансформатор «вносит» из вторичной цепи в первичную и называется вносимым сопротивлением. Можно отметить, что при достаточно малых значениях r₁, r₂, L_S1, L_S2, входное сопротивление трансформатора будет Z₁ = n² ∙ Z_Н. Таким образом, трансформатор также работает как трансформатор сопротивления, что часто используется для согласования нагрузок.

5. Потери в трансформаторе

Потери в трансформаторе складываются из потерь в обмотках на джоулево тепло и потерь в магнитопроводе на перемагничивание и вихревые токи. Умножим первое уравнение (1) на множитель i₁, а второе на i₂., результаты сложим

u₁∙i₁ = r₁ ∙ i₁² + r₂ ∙ i₂² + u₂ ∙ i₂ + L₁ ∙ i₁ ∙ (di₁ / dt) + L₂ ∙ i₂ ∙ (di₂ / dt) –

– M ∙ i₁ ∙ (di₂ / dt) – M ∙ i₂ ∙ (di₁ / dt)

или

,

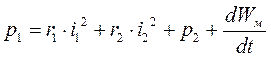где p₁ – мощность, подаваемая на вход трансформатора, p₂ – мощность, отдаваемая в нагрузку, 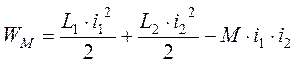 – энергия магнитного поля, запасаемая в любой момент времени в трансформаторе. Трансформатор, в котором r₁ = r₂ = 0, L_S1 = L_S2 = 0, называют идеальным. Для него L₁ = L₂ ∙ n², i₁ = i₂ / n, . Подставив эти значения в выражение для W_M, получим W_M = 0. Таким образом, в идеальном трансформаторе энергия магнитного поля в любой момент времени равна нулю. Мгновенная мощность p₁ = p₂. Потери равны нулю. В неидеальном трансформаторе мгновенная мощность не только передается нагрузке, но также частично теряется на сопротивлениях первичной и вторичной обмоток и идет на изменение энергии магнитного поля W_M. Часть энергии магнитного поля безвозвратно теряется на перемагничивании магнитопровода (потери на гистерезис) и на потери за счет вихревых токов. Эта мощность выделяется в магнитопроводе в виде тепловой мощности, которая греет трансформатор и ее надо отводить. При проектировании трансформатора необходимо учитывать свойства материала магнитопровода, которые имеют разные удельные (на килограмм массы или объем магнитопровода) потери, а также повышение потерь на сопротивлении обмоток за счет увеличения эффективных сопротивлений обмоток из-за скин-эффекта [3; 6]. Для учета мощности потерь в магнитопроводе параллельно индуктивности намагничения n ∙ M подключается сопротивление потерь в магнитопроводе рис.7.

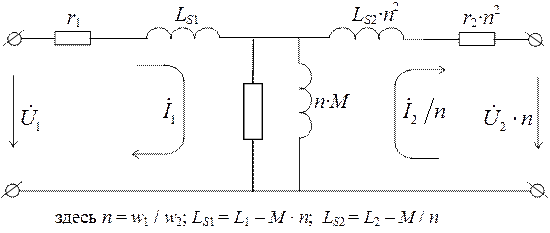
Рис. 7

Эта схема является основной для анализа работы схем с применением трансформатора на низких и средних частотах, то есть тогда, когда можно пренебречь влиянием паразитных емкостей (емкости межвитковые в обмотках, емкости между обмотками и между обмотками и элементами конструкции).

6. Практическая часть

Оборудование. Осциллограф, генератор, мультиметр с возможностью измерения индуктивности, источник питания постоянного тока регулируемый от 0 до 30 Вольт, лабораторный автотрансформатор (ЛАТР); сетевой понижающий трансформатор на 36 В; трансформатор исследуемый.

Материалы и комплектующие.

Резисторы:      МЛТ-1-10 Ом; МЛТ-2-510 ; C5-37-16-200 Ом. Все номиналы можно варьировать ± 20 %: Эти значения приняты только для удобства расчетов

Задание 1. Возьмите испытуемый трансформатор (трансформатор Т2 в схеме на рис. 8). Измерьте активные сопротивления обмоток трансформатора.