Практикум по радиоэлектронике. Трансформатор: Методические указания к лабораторной работе № 12, страница 6

где U_m – это амплитуда напряжения одиночного импульса, t - длительность импульса. То есть, если к обмотке трансформатора приложен импульс напряжения, то магнитная индукция в магнитопроводе изменится на величину ΔB с учетом знака приложенного напряжения. Так как для неискаженной передачи импульса трансформатором важно именно ΔB, то если перед прохождением основного импульса принудительно сместить начальную точку состояния магнитопровода по петле гистерезиса в положение –B_max (рис. 1), то мы выиграем по величине допустимого по свойствам материала ΔB_доп = 2 ∙ B_max, а это, в свою очередь, позволяет сэкономить на размерах и массе трансформатора.

Для синусоидального напряжения выполняется соотношение

                                   ,                                       (9)

где  – это комплекс действующего значения напряжения, приложенного к первичной обмотке, f – это частота напряжения,  – комплекс амплитуды магнитной индукции.

Уравнение (6) справедливо как при холостом ходе (i₂ = 0), так и при наличии нагрузки, т. е. при переходе от холостого хода к режиму работы при нагрузке поток Ф₁₂ практически остается неизменным по модулю. Но если в этих двух режимах поток Ф₁₂ один и тот же, то должны быть равны и создающие этот поток магнитодвижущие силы (МДС), т. е. i₁ × w₁+i₂ × w₂ = i₀ ∙ w₁, где i₀ – это ток первичной обмотки в отсутствии нагрузки.

МДС, определяющая общий магнитный поток, который пронизывает первичную и вторичную обмотки, при встречном направлении токов равна i₁ × w₁-i₂ × w₂ = (i₁-i₂/n) × w₁ = i₀∙w_1.

Ток i₁ – i₂/n и соответствующий ему комплексный ток , который в схеме замещения трансформатора, приведенной к первичной обмотке, проходит через ветвь намагничивания, принято называть намагничивающим током трансформатора. Для идеального трансформатора ток намагничивания равен нулю, индуктивности рассеяния и активные сопротивления обмоток равны нулю, u₁ / u₂ = i₂ / i₁ = n. Для реального трансформатора ток намагничивания отличается от нуля и ток, который будет потреблять трансформатор от источника энергии, складывается из тока в нагрузку I_н и тока намагничивания. Но правильно спроектированный трансформатор имеет ток намагничивания на уровне нескольких процентов от номинального тока и поэтому им можно пренебречь и на практике использовать соотношения u₁/u₂ = i₂ / i₁ = n. Связь между напряженностью магнитного поля в магнитной системе и намагничивающим током определяется законом полного тока. Для трансформатора приближенно ток намагничивания i₁ » H∙l/w₁, индукция в магнитопроводе B = µ ∙ µ₀ ∙ H. Из этих соотношений и закона электромагнитной индукции вытекает выражение для индуктивности намагничивания 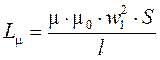, где l – это длина силовой линии магнитопровода. Здесь приведено значение индуктивности относительно первичной обмотки

Собственные сопротивления обмоток r₁ и r₂, индуктивности рассеяния L_S1 и L_S2 определяют собственное комплексное сопротивление трансфор­ма­тора. Это сопротивление для заданного входного напряжения на первичной обмотке ограничивает ток, который можно передать в нагрузку через этот трансформатор на заданной частоте w. Из эквивалентной схемы замещения видно, что это сопротивление равно

r₁ + n² ∙ r₂ + j ∙ ω ∙ (L_S1 + n² ∙ L_S2).

Для внешней цепи (относительно зажимов первичной обмотки) трансформатор вместе с нагрузкой будет представлять собой комплексное сопротивление