Практикум по радиоэлектронике. Трансформатор: Методические указания к лабораторной работе № 12, страница 5

Эти уравнения, кроме того, являются уравнениями, описывающими схему, изображенную на рис. 5.

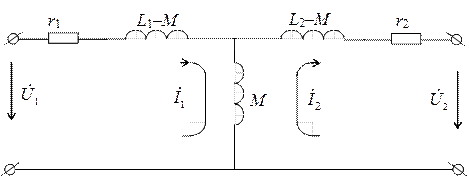
Рис. 5

Следовательно, эта схема может рассматриваться в качестве схемы замещения трансформатора. Входящие в схему разности L₁–M и L₂–M имеют физический смысл при w₁ = w₂: они представляют собой индуктивности рассеяния L_S1 и L_S2, связанные с соответствующими потоками рассеяния Ф_1S и Ф_2S, которые отражают неидеальность индуктивной связи между катушками. (Разница между полным потоком, обусловленным током i₁, и той его частью, которая пронизывает витки второй катушки, называется потоком рассеяния Ф_1S = L₁ × i₁/w₁. Аналогично для второй катушки Ф_2S = L₂ × i₂/w₂). Из схемы замещения L_S1 = L₁-M и L_S2 = L₂-M. При неодинаковых числах витков w₁ и w₂ на практике пользуются так называемой приведенной схемой замещения трансформатора, показанной на рис. 6. Приведение заключается в том, что напряжение и ток заменяются величинами, приведенными к первичной обмотке: напряжение  умножается на n, а ток  делится на n. Здесь n = w₁ / w₂ – отношение чисел витков, которое называется коэффициентом трансформации.

Придав уравнениям (2) следующий вид:

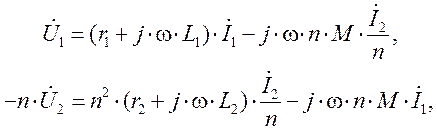                               (3)

можно преобразовать их таким образом:

(4)

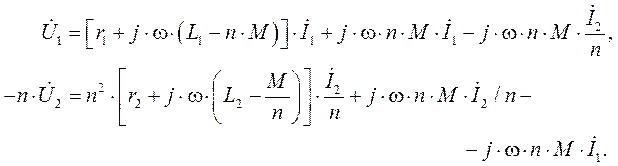
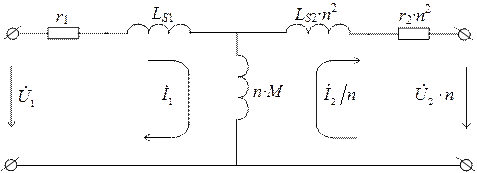
Здесь n = w₁ / w₂; L_S1=L₁–M ∙ n; L_S2=L₂–M / n

Рис. 6

Полученные уравнения являются контурными уравнениями для схемы на рис. 6 и, следовательно, эта схема является схемой замещения трансформатора. Эта схема содержит: сопротивление r₁ и индуктивность рассеяния L_S1 первичной обмотки трансформатора; индуктивность намагничивания L_µ = M × n в поперечной ветви (эта ветвь называется ветвью намагничивания); сопротивление r₂ и индуктивность рассеяния L_S2 вторичной обмотки, приведенные к первичной обмотке трансформатора. Индуктивные сопротивления L_S1 × w и L_S2 × w представляют собой сопротивления рассеяния первичной и вторичной обмоток трансформатора, а индуктивное сопротивление n × w × M - сопротивление ветви намагничивания.

4. Магнитное поле в магнитопроводе

На основе схемы рис. 6 можно записать уравнения (1) в форме

u₁ = r₁∙i₁+L_S1∙(di₁/dt)+w₁∙(dФ₁₂/dt);                           (5a)

                           –u₂ = r₂∙i₂+L_S2∙(di₂/dt)+w₂∙(dФ₁₂/dt).                          (5b)

Правильно спроектированные трансформаторы обычно имеют малые значения сопротивлений обмоток и индуктивности рассеивания, поэтому можно считать приближенно, что приложенное к первичной обмотке трансформатора напряжение уравновешивается индуцируемой в обмотке ЭДС, и поэтому

u₁ » w₁ ∙ (dФ₁₂/dt) = w₁ ∙ S ∙ (dB/dt),                            (6)

где S – площадь сечения магнитопровода, охваченного витками обмотки, B – индукция в магнитопроводе. Интегрируя это равенство, получим

,

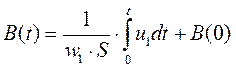где B(0) – некоторое начальное значение индукции в магнитной системе, соответствующее моменту времени t = 0.

При практических расчетах обычно интересуются не абсолютным значением индукции в магнитопроводе, а ее приращением во времени. Поэтому это выражение удобно переписать в виде

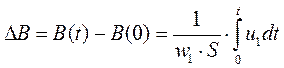                              .                               (7)

Для импульсного напряжения произвольной формы интеграл берется по длительности импульса, причем принимается, что интервал следования импульсов достаточно велик, чтобы закончились все переходные процессы и трансформатор успел вернуться в исходное состояние.

Для одиночного прямоугольного импульса тогда получится

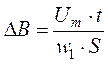                                                ,                                                (8)