


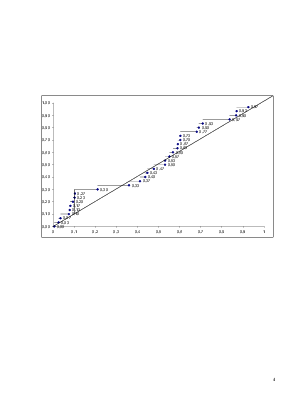
Задача 1.
Построить точно доверительный интервал для параметра нормального распределения уровня доверия 1-e по исходной выборке объема 50.
а) а, если s2 известно
Решение:
![]() ,
,
Статистика 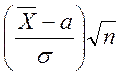 имеет распределение
имеет распределение ![]() , где
, где 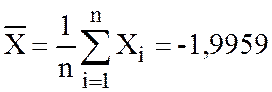 ,
поэтому, если
,
поэтому, если 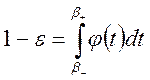 , то
, то 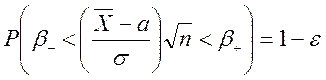 ,
следовательно, по определению доверительного интервала уровня доверия 1-e получаем, что
,
следовательно, по определению доверительного интервала уровня доверия 1-e получаем, что ![]() -
доверительный интервал для
-
доверительный интервал для 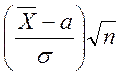 , значит, для а
доверительный интервал:
, значит, для а
доверительный интервал: 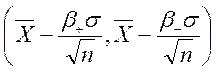
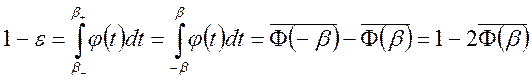
![]()
Ответ: доверительный интервал уровня доверия 1-e для а, если s2 известно:
![]()
б) а, если s2 неизвестно
Решение:
Статистика 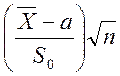 имеет распределение
имеет распределение ![]() , где
, где 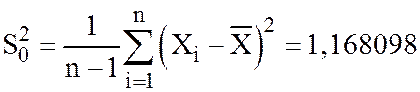 ,
, 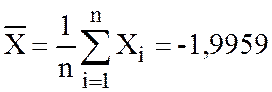 , (степеней свободы 49) поэтому, если
, (степеней свободы 49) поэтому, если 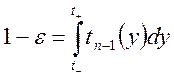 , то
, то 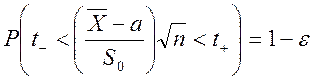 ,
следовательно, по определению доверительного интервала уровня доверия 1-e получаем, что
,
следовательно, по определению доверительного интервала уровня доверия 1-e получаем, что ![]() -
доверительный интервал для
-
доверительный интервал для 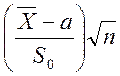 , значит, для а
доверительный интервал:
, значит, для а
доверительный интервал:
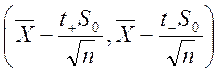
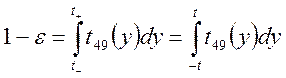
Поэтому, 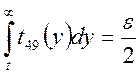 , по справочным таблицам находим:
, по справочным таблицам находим: ![]()
Ответ: доверительный интервал уровня доверия 1-e для а, если s2 неизвестно:
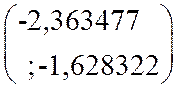
в) s2, если а известно
Решение: Статистика 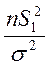 имеет распределение
имеет распределение ![]() , где
, где 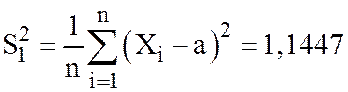 ,
поэтому, если
,
поэтому, если 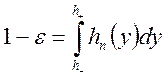 , то
, то 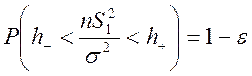 ,
следовательно, по определению доверительного интервала уровня доверия 1-e получаем, что
,
следовательно, по определению доверительного интервала уровня доверия 1-e получаем, что ![]() -
доверительный интервал для
-
доверительный интервал для 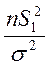 , значит, для s2 доверительный интервал:
, значит, для s2 доверительный интервал: 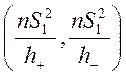
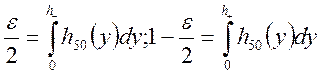
Поэтому, по
справочным таблицам находим: ![]()
Ответ: доверительный интервал уровня доверия 1-e для s2, если а известно:
![]()
г) s2, если а неизвестно
Решение:
Статистика 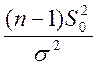 имеет распределение
имеет распределение ![]() , где
, где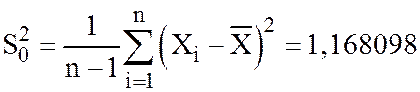 ,
, 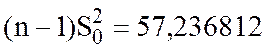 , поэтому, если
, поэтому, если 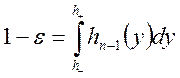 , то
, то 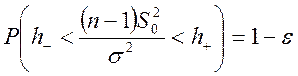 , следовательно, по определению
доверительного интервала уровня доверия 1-e
получаем, что
, следовательно, по определению
доверительного интервала уровня доверия 1-e
получаем, что ![]() - доверительный интервал для
- доверительный интервал для 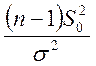 , значит, для s2 доверительный интервал:
, значит, для s2 доверительный интервал:
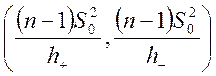
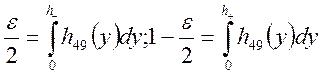
Поэтому, по
справочным таблицам находим: ![]()
Ответ: доверительный интервал уровня доверия 1-e для s2, если а неизвестно:
![]()
Задача 2
По данным числовым наблюдениям (выборка объема 30) проверить основную гипотезу о равномерности распределения с помощью:
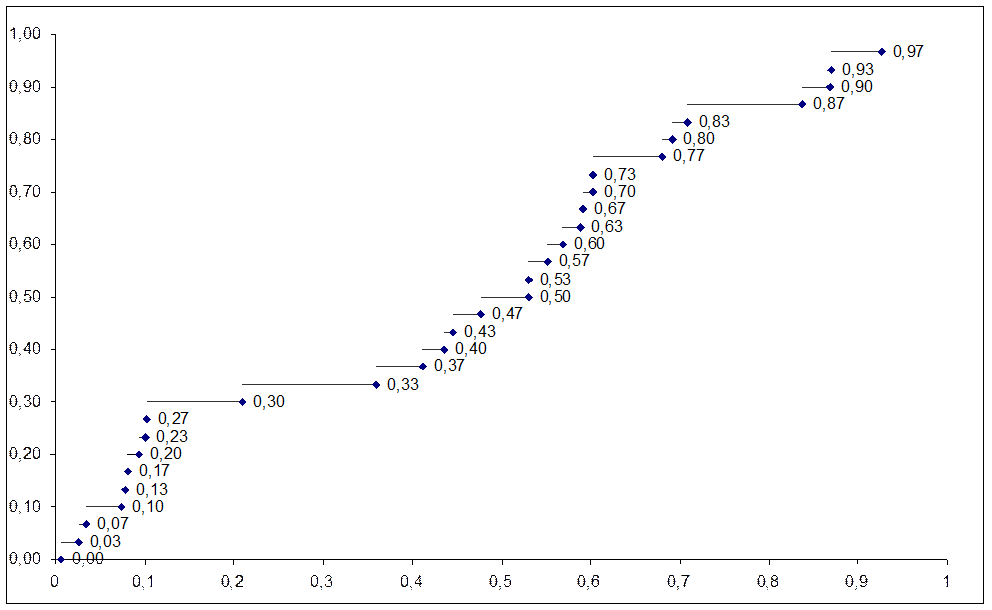
а) критерия Колмогорова
Решение:
![]()
![]()
Рассмотрим
статистику 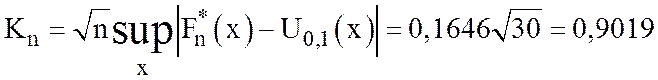
![]() , где
, где 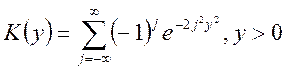 -
функция Колмогорова.
-
функция Колмогорова.
По критерию
Колмогорова ![]() отвергается, если
отвергается, если ![]() ,
и принимается, если
,
и принимается, если ![]()
По справочным
таблицам находим: ![]() , следовательно,
, следовательно, ![]()
Ответ: основная гипотеза принимается на основании критерия Колмогорова.
б) критерия хи-квадрат
Решение:
![]()
|
|
интервалы |
|
сумма |
|
1 |
0-0,1 |
7 |
5,3333333 |
|
2 |
0,1-0,2 |
2 |
0,333333 |
|
3 |
0,2-0,3 |
1 |
1,333333 |
|
4 |
0,3-0,4 |
1 |
1,333333 |
|
5 |
0,4-0,5 |
4 |
0,333333 |
|
6 |
0,5-0,6 |
6 |
3 |
|
7 |
0,6-0,7 |
4 |
0,333333 |
|
8 |
0,7-0,8 |
1 |
1,333333 |
|
9 |
0,8-0,9 |
3 |
0 |
|
10 |
0,9-1 |
1 |
1,333333 |
|
|
14,666667 |
||
![]() – количество
– количество ![]() ,
попавших в
,
попавших в ![]()
Рассмотрим статистику 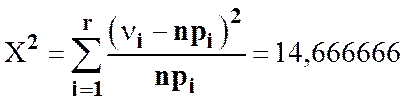
По критерию
Пирсона (хи-квадрат) ![]() отвергается, если
отвергается, если ![]() , и принимается, если
, и принимается, если ![]() , где
, где ![]() квантиль
уровня 1-e для распределения
квантиль
уровня 1-e для распределения ![]() , т.е.
, т.е. 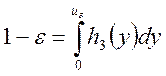
По справочным
таблицам находим: ![]() , следовательно,
, следовательно, ![]()
Ответ: основная гипотеза принимается на основании критерия хи-квадрат.
Задача 3.
а) Проверить гипотезу о совпадении дисперсий при неизвестных средних,
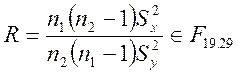 – распределение Фишера,
– распределение Фишера,
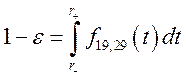 ,
, 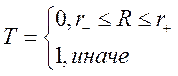
r- = 0,398472, r+ = 2,319879, R = 1,579765,
r- < R < r+
Ответ: основная гипотеза принимается
б) Проверить гипотезу о совпадении средних, если известно, что неизвестные дисперсии совпадают,
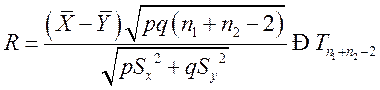 ,
, 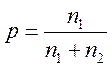 ,
, ![]() ,
,
![]() :
: 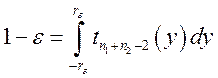 ,
, 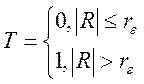
rτ =2,111073, ![]() ,
, ![]() , |R| = 0,773260;
, |R| = 0,773260;
|R| <rτ
Ответ: основная гипотеза принимается
![]()

Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.