Задача: построить приближённую функцию g(x) методом наименьших квадратов, используя в качестве базовых функций набор одночленов pj=x^j
Метод: требуется найти функцию g(x): //f(x)-g(x)// = inf //f(x)-g(x)//=v
Аппроксимирующую функцию
берём в виде линейной комбинации: g(x)=![]() cj*pj(x).
cj*pj(x).
Подставляем в //f(x)-g(x)//^2 и дифференцируем.
Получаем ![]() (pm,pj)cj=(f,pm).
(pm,pj)cj=(f,pm).
Получаем матрицу коэффициентов, которую решаем методом Гаусса, проверив сначала угловые миноры, чтобы метод сработал нормально. Из матрицы находим коэффициенты cj.
Рассмотрим функцию f(x)=x^3-5*x
x1=0 x2=1 x3=3 x4=4
f(x1)=0 f(x2)=-4 f(x3)=12 f(x4)=44
Получаем коэффициенты cj: 0 -5 0 1
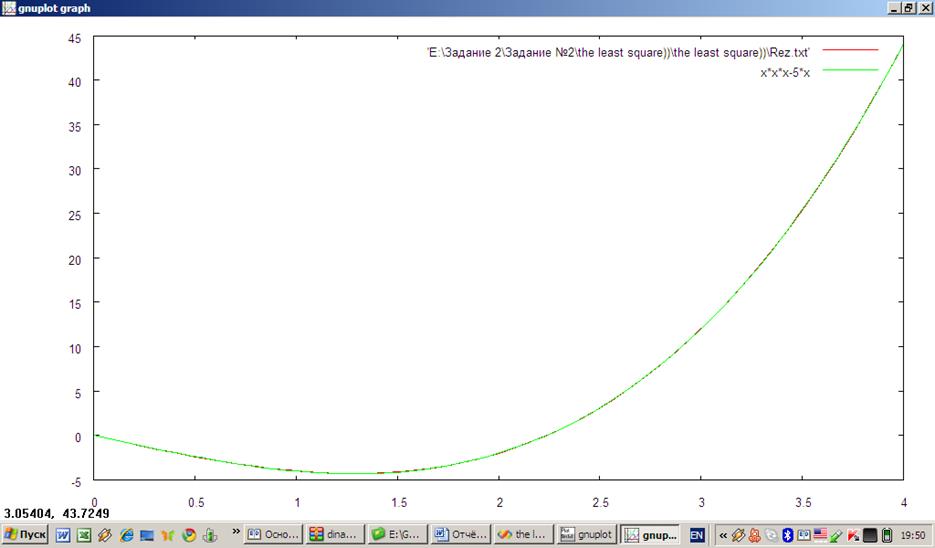
- получаем достаточно точное приближение.
Рассмотрим функцию f(x)=3
x1= 1 x2=2 x3=5 x4=9
f(x1)=3 f(x2)=3 f(x3)=3 f(x4)=3
Получаем коэффициент cj=3
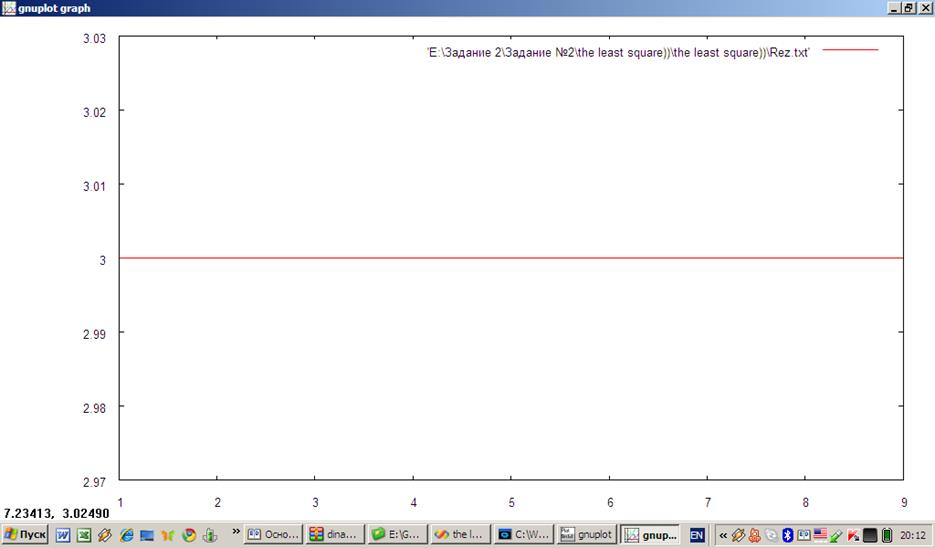
- получаем точное совпадение.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.