Написание программы, решающей уравнение Ах=b итерационным методом релаксации с заданным параметром w

Задание № 3

Написать программу, решающую уравнение  итерационным методом релаксации с заданным параметром w,  для симметричной положительно определенной матрицы  и вектора b, решающую полную проблему собственных значений матрицы  итерационным методом Якоби.

Методы и алгоритмы:

Метод релаксации:  каждый следующий значение в столбце  находим из  и уже вычисленных значений  следующим образом:

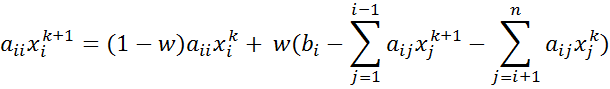
где i=1,…n; j=0,1,…  

При w=1 получаем метод Гаусса – Зейделя.

Итерационный метод Якоби – выбираем ненулевой элемент  матрицы , обнуляем  с помощью матриц вращения. При таких преобразованиях другие элементы матрицы меняются, но фробениусова норма внедиагональной части матрицы уменьшается. В итоге получим матрицу с собственными числами на диагонали.

Примеры вычислений:

1) Для заданной точности  найдем решение системы

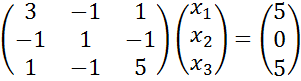
с начальным приближением (0,0,0) программа выдает верное  решение:

,  и собственные числа  за 14 и 7 итераций.

2) Для заданной точности  найдем решение системы

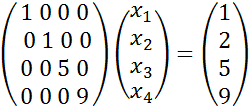
с начальным приближением (1,5,9,5) программа выдает верное решение:

, ,   и собственные числа ,  за 2 и 0 итераций.

3) Для заданной точности  найдем решение системы

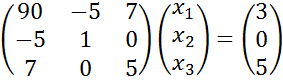
с начальным приближением (0,0,0) программа выдает верное решение:

,  и собственные числа  за 55 и 6 итераций.