Неоднородные линейные уравнения с постоянными коэффициентами

2)         Неоднородные линейные уравнения с постоянными

коэффициентами

1º. НЛДУ с постоянными коэффициентами – уравнение (6.1), в котором коэффициенты при помощи метода вариации произвольных постоянных всегда может быть проинтегрировано в квадратурах от элементарных функций, ибо соответствующее ему ОЛДУ (6.2) с постоянными коэффициентами имеет ФСР, состоящую из элементарных функций (п.10.6.2. (1)).

Пример 1. Найти общее решение уравнения .

Решение. ФСР соответствующего ОЛДУ , полученная по методу Эйлера, состоит из функций: . Для нахождения общего решения НЛДУ воспользуемся методом вариации произвольных постоянных. Составим систему (6.9):

                                           

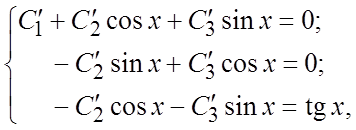
откуда алгебраическим путем определим: .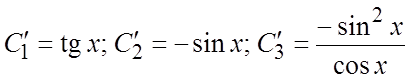

Интегрирование дает:   

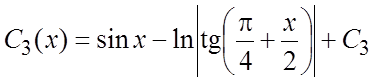и общее решение имеет вид:

.

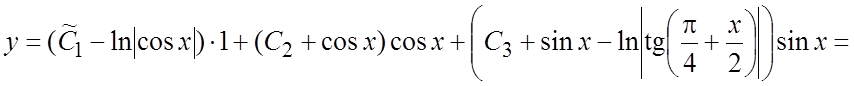
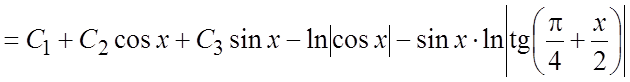2^°. В некоторых случаях для НЛДУ с постоянными коэффициентами удается найти частное решение методом неопределенных коэффициентов, исходя из заранее известного вида последнего – для НЛДУ с постоянными коэффициентами с правой частью специального вида. Укажем эти случаи и соответствующие им виды частных решений.

1) , где   - многочлен от x; в частности, это может быть число . Тогда а) если число 0 не является корнем характеристического уравнения (6.11), то частное решение НЛДУ можно найти в виде

                                                               ,                                               (6.12)

где - многочлен той же степени, что и , но с неопределенными (подлежащими определению путем подстановки (6.12) в НЛДУ) коэффициентами; б) если 0 есть корень уравнения (6.11) кратности k, то

                                                              .                                          (6.12¢)

2) . Если число a не является корнем характеристического уравнения (6.11), то

                                                             .                                            (6.13)

Если a – корень (6.11) кратности k, то

                                                           .                                     (6.13¢)

3) , где  и  -  многочлены от x. Эти многочлены, в частности, могут быть постоянными числами, и один из них может быть тождественным нулем. Пусть m есть наивысшая из степеней многочленов  и . Тогда а) если число  не является корнем (6.11), то

                                      ,                            (6.14)

где  и - многочлены степени m с неопределенными коэффициентами;

б) если есть корень характеристического уравнения (6.11) кратности k, то

                                        .                     (6.14¢)

4)  где  - функции вида, рассмотренного в пп. 1-3. Если  есть частные решения соответствующие НЛДУ с правыми частями , то

                                                                                        (6.15)

является частным решением всего (исходного) уравнения (6.1) (см. принцип суперпозиции, п.2, § 10.6.1).

Пример 6. Проинтегрировать уравнение .

Решение. 1)найдем общее решение соответствующего ему ОЛДУ. Характеристическое уравнение  имеет различные корни:  и общее решение ОЛДУ: .

2) здесь - многочлен второго порядка. Так как число ноль не является корнем характеристического уравнения, частное решение ищем в виде (6.12):  - неизвестные, подлежащие определению, коэффициенты. Подставляя y в исходное НЛДУ, получим: , откуда, сравнивая коэффициенты при одинаковых степенях x, получим систему уравнений: – . Решая ее, найдем:  и частное решение имеет вид: . По формуле (6.7) общее решение исходного уравнения имеет вид: .

Пример 7. В каком виде следует искать частое решение НЛДУ ?

Решение. Характеристическое уравнение  имеет корни . Так как число 0 есть двукратный корень характеристического уравнения, то частное решение следует искать по рекомендации (6.12¢):

.

Ответ. .

Пример 8. Проинтегрировать уравнение .