Решение. 1). Характеристическое уравнение ![]() имеет
двукратный корень
имеет
двукратный корень ![]() , поэтому
, поэтому ![]() .
2). Здесь
.
2). Здесь ![]()
![]() . Так как a = –5 является корнем характеристического уравнения
кратности k = 2, то частное решение
. Так как a = –5 является корнем характеристического уравнения
кратности k = 2, то частное решение ![]() НЛДУ ищем по формуле (6.13¢):
НЛДУ ищем по формуле (6.13¢): ![]() . Тогда
. Тогда
![]() ,
, ![]() .
.
Подставляя ![]() и
и ![]() в
исходное уравнение, получим
в
исходное уравнение, получим ![]() , откуда
, откуда ![]() и
и ![]() . Общее
решение исходного НЛДУ:
. Общее
решение исходного НЛДУ: ![]() .
.
Пример 9. Найти общее решение уравнения ![]() .
.
Решение. 1). Характеристическое уравнение ![]() имеет
корни
имеет
корни ![]() ,
, ![]() ,
поэтому
,
поэтому ![]() . 2). Здесь
. 2). Здесь ![]() .
Характеристика
.
Характеристика ![]() не является корнем
характеристического уравнения; для определения частного решения используем
рекомендацию (6.14). Определим m:
не является корнем
характеристического уравнения; для определения частного решения используем
рекомендацию (6.14). Определим m: ![]() и , таким образом,
и , таким образом, ![]() . Найдем
. Найдем ![]() и
и ![]() и подставим
и подставим ![]() и
и ![]() в заданное уравнение; получим, собрав в
левой части отдельно члены при cosx, отдельно
при sinx:
в заданное уравнение; получим, собрав в
левой части отдельно члены при cosx, отдельно
при sinx: ![]()
![]()
![]()
![]() .
Сравнивая отдельно выражения при cosx и при sinx слева и справа, придем к системе уравнений:
.
Сравнивая отдельно выражения при cosx и при sinx слева и справа, придем к системе уравнений:
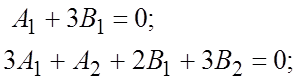
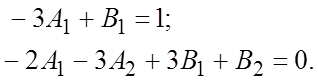
Решая, получим ![]() и частное решение
и частное решение 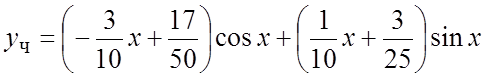 .
Общее решение запишется по формуле (6.7):
.
Общее решение запишется по формуле (6.7): 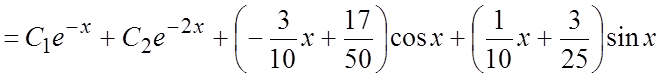 .
.
Пример 10. Проинтегрировать уравнение ![]() .
.
Решение. 1). Найдем общее решение соответствующего ОЛДУ: ![]() ,
, ![]() ,
, ![]()
![]() . 2).Частное решение
уравнения
. 2).Частное решение
уравнения ![]() (1) следует искать в виде (6.14¢), так как характеристика
(1) следует искать в виде (6.14¢), так как характеристика ![]() является простым корнем
характеристического уравнения :
является простым корнем
характеристического уравнения :![]() .
.
Подставляя ![]() в уравнение (1), получим:
в уравнение (1), получим: ![]() , откуда
, откуда 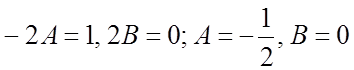 и
и 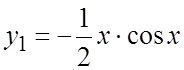 . Для уравнения
. Для уравнения ![]() (2)
имеем
(2)
имеем ![]() - используем формулу (6.14), ибо здесь
- используем формулу (6.14), ибо здесь ![]() не является корнем характеристического
уравнения. Подставляя
не является корнем характеристического
уравнения. Подставляя ![]() в (2), найдем
в (2), найдем 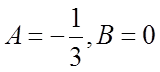 , так что
, так что 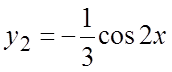 .
Используя формулу (6.7) и принцип суперпозиции частных решений, запишем общее
решение НЛДУ:
.
Используя формулу (6.7) и принцип суперпозиции частных решений, запишем общее
решение НЛДУ: 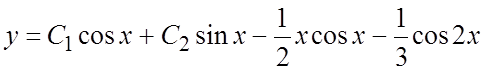 .
.
Пример 11. Найти общее решение НЛДУ ![]() .
.
Решение. 1). Характеристическое уравнение ![]() имеет
корни
имеет
корни ![]() , так что
, так что ![]() .
2).Здесь
.
2).Здесь ![]() и так как характеристика
и так как характеристика ![]() является простым корнем
характеристического уравнения, частное решение надо искать в виде (6.14¢):
является простым корнем
характеристического уравнения, частное решение надо искать в виде (6.14¢): ![]() ; тогда
; тогда
![]()
![]() ,
,![]()
![]() . Подставляя
. Подставляя ![]() и
и ![]() в
исходное уравнение и сокращая на
в
исходное уравнение и сокращая на ![]() , получим
, получим ![]() ,откуда
,откуда ![]() и
и ![]() . Общее решение НЛДУ:
. Общее решение НЛДУ: ![]()
![]() .
.
Исследовать на линейную зависимость в области их совместного определения системы функций:
124. ![]() ; 125.
; 125. ![]() 126.
126. ![]() ; 127.
; 127.![]() ; 128.
; 128. ![]() ; 129.
; 129. ![]() . 130.
. 130.
![]() ; 131.
; 131. ![]() ;
;
132. ![]() ; 133.
; 133.
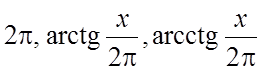 .
.
В задачах 134-139 найти определитель Вронского для указанных систем функций:
134. ![]() ; 135.
; 135. ![]() 136.
136. ![]() 137.
137. ![]() 138.
138. ![]()
139. ![]() .
.
По заданной ФСР ОЛДУ составить это уравнение:
140. ![]() 141.
141. ![]() 142.
142. ![]() 143.
143. ![]() 144.
144. ![]()
145. ![]() 146.
146. ![]() 147.
147. ![]() .
.
Найти общее решение ОЛДУ, если известно одно частное решение:
148. ![]() ; 149.
; 149. ![]()
150. 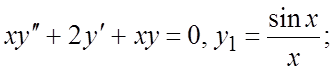 151.
151. ![]() ;
;
152. ![]()
153. ![]()
154. ![]()
В нижеследующих
НЛДУ, зная одно частное решение ![]() соответствующего ОЛДУ и
угадав некоторое частное решение
соответствующего ОЛДУ и
угадав некоторое частное решение ![]() НЛДУ, либо применив
метод вариации произвольных постоянных, найти общее решение:
НЛДУ, либо применив
метод вариации произвольных постоянных, найти общее решение:
155. 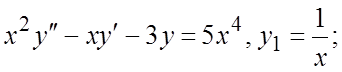 156.
156. ![]()
157. ![]()
158. 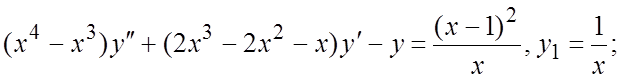
159.![]()
160.![]()
В уравнениях
161-165 частным решением ОЛДУ является ![]() :
:
161. 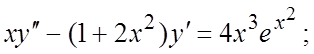 162.
162. ![]() 163.
163. ![]()
164. ![]() 165.
165. ![]() .
.
Проинтегрировать следующие ОЛДУ с постоянными коэффициентами:
166.![]() 167.
167.![]() 168.
168.![]()
169.![]() 170.
170.![]() 171.
171.![]()
172.![]() 173.
173.![]() 174.
174.![]() 175.
175.![]()
176.![]() 177.
177.![]() 178.
178.![]()
179.![]() 180.
180.![]()
181.![]() 182.
182.![]()
183.![]() 184.
184. ![]()
Методом вариации произвольных постоянных решить следующие НЛДУ с постоянными коэффициентами:
185. ![]() 186.
186. 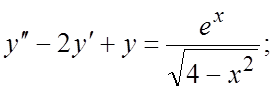 187.
187. 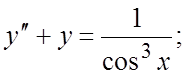
188.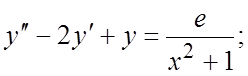 189.
189. 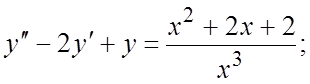 190.
190.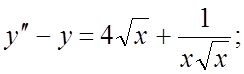
191.![]() 192.
192. 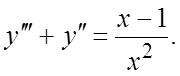
Определить вид
частного решения НЛДУ, если известны корни его характеристического уравнения и
правая часть ![]() - функция специального вида:
- функция специального вида:
193. ![]() 194.
194. ![]()
195. ![]() 196.
196. ![]()
197. ![]() 198.
198. ![]()
199. ![]()
200. ![]()
201. ![]() .
.
Пользуясь принципом суперпозиции, определить вид частного решения следующих НЛДУ:
202.![]() 203.
203.![]() 204.
204.![]()
205.![]() 206.
206.![]() 207.
207.![]()
208.![]() 209.
209. ![]()
Проинтегрировать следующие НЛДУ, найдя предварительно их частные решения методом неопределенных коэффициентов:
210.![]() 211.
211.![]() 212.
212.![]()
213.![]() 214.
214.![]() 215.
215.![]() 216.
216. ![]()
217.![]() 218.
218.![]()
219.![]() 220.
220.![]() 221.
221.![]() 222.
222.![]() 223.
223.![]() 224.
224.![]() 225.
225.![]() 226.
226.![]() 227.
227.![]() 228.
228.![]() 229.
229.![]()
230.![]() 231.
231. ![]()
232. ![]() 233.
233.![]()
234.![]() 235.
235. ![]() 236.
236.
![]()
237. ![]() 238.
238. ![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.