Эквивалентные
функции. Функции f(x) и g(x) называются эквивалентными при 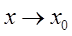 , если , если 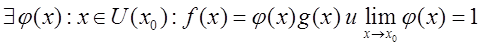 . .
Функции одного порядка. Если даны функции f(x) и g(x)
такие, что 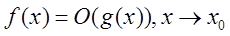 и и 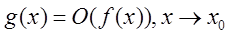 , то они называются функциями одного порядка: , то они называются функциями одного порядка: 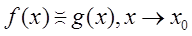
Критерий
Коши для непрерывной функции. Для того чтобы функция f(x) имела в точке x конечный
предел, необходимо и достаточно, чтобы для 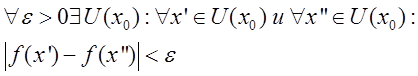 . .
Теорема
Вейерштрассе. Всякая
непрерывная на отрезке функция ограничена и достигает на этом отрезке своей
верхней и нижней грани.
Теорема
Больцано-Коши. Если
функция f(x)
непрерывна на [a, b], 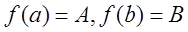 , то , то 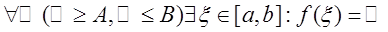 . Т.е. непрерывная функция, принимающая на отрезке
какие-либо два значения, принимает и любое значение между ними. . Т.е. непрерывная функция, принимающая на отрезке
какие-либо два значения, принимает и любое значение между ними.
Равномерная
непрерывность.
Функция f(x),
определенная на
множестве X, называется равномерно непрерывной
на множестве X, если 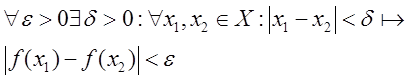
Теорема Кантора. Всякая непрерывная на компакте функция равномерно
непрерывна на нем.
|
Эквивалентные
функции. Функции f(x) и g(x) называются эквивалентными при 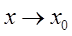 , если , если 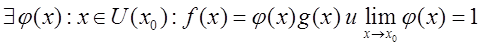 . .
Функции одного порядка. Если даны функции f(x) и g(x)
такие, что 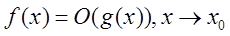 и и 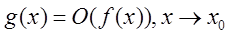 , то они называются функциями одного порядка: , то они называются функциями одного порядка: 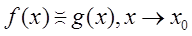
Критерий
Коши для непрерывной функции. Для того чтобы функция f(x) имела в точке x конечный
предел, необходимо и достаточно, чтобы для 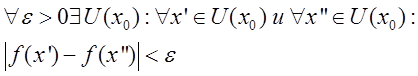 . .
Теорема
Вейерштрассе. Всякая
непрерывная на отрезке функция ограничена и достигает на этом отрезке своей
верхней и нижней грани.
Теорема
Больцано-Коши. Если
функция f(x)
непрерывна на [a, b], 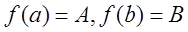 , то , то 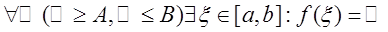 . Т.е. непрерывная функция, принимающая на отрезке
какие-либо два значения, принимает и любое значение между ними. . Т.е. непрерывная функция, принимающая на отрезке
какие-либо два значения, принимает и любое значение между ними.
Равномерная
непрерывность.
Функция f(x),
определенная на множестве
X, называется равномерно непрерывной на множестве X, если 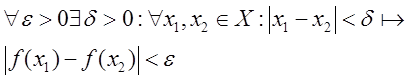
Теорема Кантора. Всякая непрерывная на компакте функция равномерно
непрерывна на нем.
|
Эквивалентные
функции. Функции f(x) и g(x) называются эквивалентными при 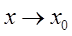 , если , если 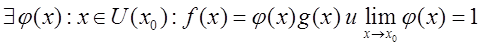 . .
Функции одного порядка. Если даны функции f(x) и g(x)
такие, что 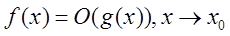 и и 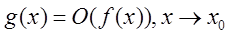 , то они называются функциями одного порядка: , то они называются функциями одного порядка: 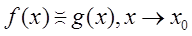
Критерий
Коши для непрерывной функции. Для того чтобы функция f(x) имела в точке x конечный
предел, необходимо и достаточно, чтобы для 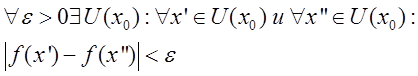 . .
Теорема
Вейерштрассе. Всякая
непрерывная на отрезке функция ограничена и достигает на этом отрезке своей
верхней и нижней грани.
Теорема
Больцано-Коши. Если
функция f(x)
непрерывна на [a, b], 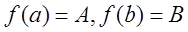 , то , то 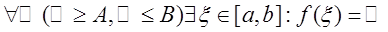 . Т.е. непрерывная функция, принимающая на отрезке
какие-либо два значения, принимает и любое значение между ними. . Т.е. непрерывная функция, принимающая на отрезке
какие-либо два значения, принимает и любое значение между ними.
Равномерная
непрерывность.
Функция f(x),
определенная на
множестве X, называется равномерно непрерывной
на множестве X, если 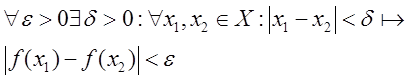
Теорема Кантора. Всякая непрерывная на компакте функция равномерно
непрерывна на нем.
|
Эквивалентные
функции. Функции f(x) и g(x) называются эквивалентными при 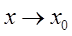 , если , если 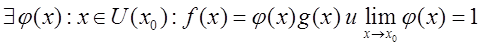 . .
Функции одного порядка. Если даны функции f(x) и g(x)
такие, что 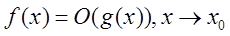 и и 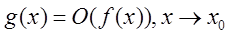 , то они называются функциями одного порядка: , то они называются функциями одного порядка: 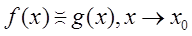
Критерий
Коши для непрерывной функции. Для того чтобы функция f(x) имела в точке x конечный
предел, необходимо и достаточно, чтобы для 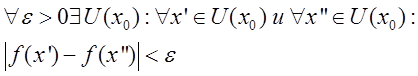 . .
Теорема
Вейерштрассе. Всякая
непрерывная на отрезке функция ограничена и достигает на этом отрезке своей
верхней и нижней грани.
Теорема
Больцано-Коши. Если
функция f(x)
непрерывна на [a, b], 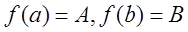 , то , то 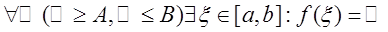 . Т.е. непрерывная функция, принимающая на отрезке
какие-либо два значения, принимает и любое значение между ними. . Т.е. непрерывная функция, принимающая на отрезке
какие-либо два значения, принимает и любое значение между ними.
Равномерная
непрерывность.
Функция f(x),
определенная на
множестве X, называется равномерно непрерывной
на множестве X, если 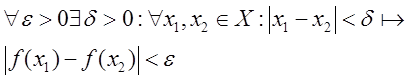
Теорема Кантора. Всякая непрерывная на компакте функция равномерно
непрерывна на нем.
|