Обыкновенные дифференциальные уравнения. Основные понятия и определения

Глава 10

Обыкновенные дифференциальные уравнения

10.1.    Основные понятия и определения

Определение 1. Обыкновенным дифференциальным уравнением (ДУ) называется равенство, содержащее независимую переменную x, неизвестную функцию y и ее производные         

                                        .                                         (1.1)

Уравнение (1.1) называется уравнением в общем виде.

Определение 2. Порядком уравнения называется порядок старшей производной, входящей в уравнение.

Определение 3. Уравнение, разрешенное относительно старшей входящей в него производной

                                                                                         (1.2)

называется уравнением n-го порядка в нормальной форме.

Определение 4. Решением уравнения (1.1) (или (1.2)) называется функция , обращающая это уравнение в тождество. График решения на плоскости Oxy называется интегральной кривой.

Замечание. Если искомая функция есть функция одной независимой переменной x, дифференциальное уравнение называется обыкновенным; иначе оно называется уравнением в частных производных. Здесь рассматриваем только обыкновенные дифференциальные уравнения.

10.2.    Дифференциальные уравнения первого порядка

Отметим записи уравнения первого порядка:

                                                                                                          (2.1)

- уравнение первого порядка в общем виде;   

                                                                                                             (2.2)

- в нормальной форме;              

                                                                                      (2.3)

- уравнение первого порядка в дифференциальной форме. 

          Ниже излагаются методы решения уравнений (2.2) и (2.3). Наряду с уравнением (2.2) рассматривается “перевернутое” уравнение

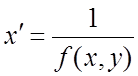                                                           .                                                    (2.2¢)

          Определение 1. Под областью определения уравнения (2.2) понимают объединение областей функций f и . Решения уравнения (2.2¢) присоединяются  к решениям уравнения (2.2).

          Пример. К решениям  уравнения  следует присоединить решение x=0 перевернутого уравнения .

          Геометрический смысл уравнения (2.2) заключается в задании в каждой точке плоскости Oxy направления касательных к интегральным кривым . Дифференциальное уравнение (2.2) задает на плоскости Oxy поле направлений.

          Задачей Коши называют задачу нахождения решения  уравнения (2.2), удовлетворяющего начальному условию . Геометрически это означает, что ищется интегральная кривая, проходящая через заданную точку  плоскости Oxy.

          Теорема существования и единственности решения задачи Коши. Пусть в (2.2) функция f(x,y) определена в некоторой области D плоскости Oxy, содержащей точку  . Задача Коши имеет и притом единственное решение (на некотором интервале , если функция f(x,y) и частная производная ее  непрерывны в области D.

          Замечание1. Существуют и другие достаточные условия существования решения и его единственности.

          Определение 2. Решение уравнения (2.2)

                                                           ,                                               (2.4)

где функция определена в некоторой области изменения переменных x и C и имеет непрерывную частную производную по x, называется общим решением уравнения (2.2) в заданной области D изменения переменных x и y, если в каждой точке этой области решение задачи Коши существует и единственно. Иначе, общее решение  дифференциального уравнения (2.2) это 1) решение; 2) какие бы начальные условия  не задать,  такое, что эти начальные условия будут удовлетворены ( то есть уравнение  разрешимо относительно С).

          Замечание 2. Если общее решение уравнения (2.2) задано в неявном виде

                                                        ,                                                    (2.5)

то оно называется общим интегралом этого уравнения.

          Определение 3. Решение, в каждой точке которого сохраняется единственность решения задачи Коши, называется частным решением.

          Определение 4. Решение, в каждой точке которого нарушается единственность решения задачи Коши, называется особым решением.

          Особое решение всегда можно обнаружить в процессе построения общего решения данного дифференциального уравнения. Это те интегральные кривые, которые могут быть утеряны при преобразовании данного уравнения в процессе решения.

          Замечание 3. Кроме указанных выше, дифференциальное уравнение может иметь решения, которые не являются ни частными, ни особыми. Например, такими решениями будут решения, склеенные из “отрезков” частных и особых решений.