Глава 3. Непрерывность функции.
Число
A называется пределом функции ![]() в
точке
в
точке ![]() справа (слева) и пишут
справа (слева) и пишут 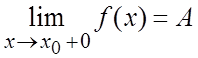
 , если
для любого
, если
для любого ![]() существует число
существует число ![]() такое,
что из условия
такое,
что из условия ![]()
![]() следует
следует
![]() . Будем также предел справа (слева)
обозначать
. Будем также предел справа (слева)
обозначать ![]()
![]() .
.
Пусть т. ![]() из области определения функции
из области определения функции ![]() . Функция
. Функция ![]() называется
непрерывной в т.
называется
непрерывной в т. ![]() , если выполняется одно из
следующих трех условий:
, если выполняется одно из
следующих трех условий:
1)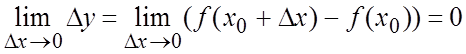 ; 2)
; 2)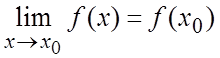 ;
;
3)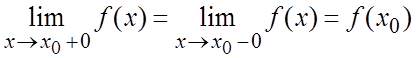 .
.
Эти условия равносильные.
Все основные элементарные функции непрерывны на своей естественной области определения.
Сумма, разность, произведение, частное и композиция конечного числа непрерывных функций есть функция непрерывная.
Функция ![]() называется непрерывной на
множестве E , если она непрерывна в каждой точке
данного множества.
называется непрерывной на
множестве E , если она непрерывна в каждой точке
данного множества.
Типы разрывов
функции в точке. а) Пусть существуют конечные пределы ![]() и
и ![]() ,
причем
,
причем ![]() =
=![]() , но не
равны
, но не
равны ![]() , либо
, либо ![]() не
определена. Тогда
не
определена. Тогда ![]() называется точкой устранимого
разрыва функции.
называется точкой устранимого
разрыва функции.
б) Пусть ![]() и
и ![]() существуют,
конечны, но не равны между собой. Тогда в т.
существуют,
конечны, но не равны между собой. Тогда в т. ![]() у
функции разрыв типа скачок. Устранимый разрыв и скачок называются
разрывами первого рода. Во всех остальных случаях точка
у
функции разрыв типа скачок. Устранимый разрыв и скачок называются
разрывами первого рода. Во всех остальных случаях точка ![]() есть точка разрыва второго рода,
т.е. если хотя бы один из односторонних пределов равен
есть точка разрыва второго рода,
т.е. если хотя бы один из односторонних пределов равен ![]() или
не существует.
или
не существует.
Пример. Исследовать на непрерывность функцию 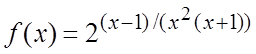 .
.
Ñ Точками возможного разрыва являются ![]() и
и ![]() .
Вычислим односторонние пределы.
.
Вычислим односторонние пределы.
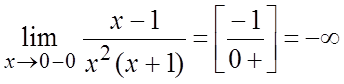 ;
; 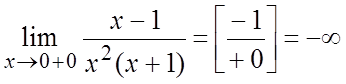 .
.
Следовательно, в
т. ![]() у функции разрыв устранимый, так как
у функции разрыв устранимый, так как 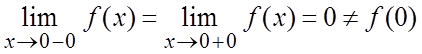 ,
,
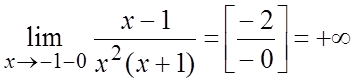 ;
; 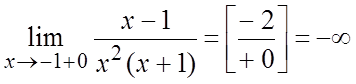 .
.
Тогда 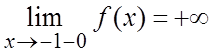 и
и 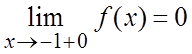 .
.
В точке ![]()
![]() имеет разрыв второго
рода. #
имеет разрыв второго
рода. #
Найти точки разрыва функции, определить их характер и построить схематично график функции в окрестности точек разрыва.
1.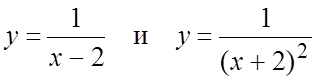 . 2.
. 2.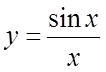 и
и 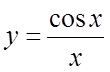 . 3.
. 3.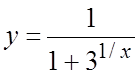 .
4.
.
4.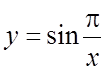 . 5.
. 5.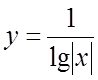 . 6.
. 6. . 7.
. 7.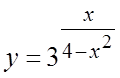 . 8.
. 8.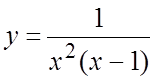 .
.
9. Функция 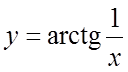 не определена в точке
не определена в точке ![]() . Можно ли так доопределить функцию
. Можно ли так доопределить функцию ![]() в точке
в точке ![]() , чтобы
функция стала непрерывной в этой точке? Построить график этой функции.
, чтобы
функция стала непрерывной в этой точке? Построить график этой функции.
10. Исследовать
характер разрыва функции 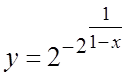 в точке
в точке ![]() . Можно ли так доопределить
. Можно ли так доопределить ![]() при
при ![]() , чтобы
функция стала непрерывной при
, чтобы
функция стала непрерывной при ![]() ?
?
Исследовать на непрерывность функции. Сделать чертеж графика.
11. 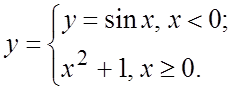 12.
12.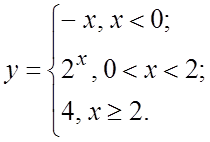 13.
13. 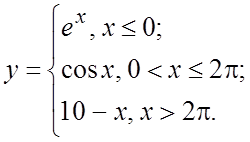
14.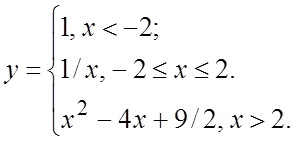
Ответы к задачам главы 3:
1. Функция ![]() имеет в точке
имеет в точке ![]() разрыв
второго рода (бесконечный,
разрыв
второго рода (бесконечный, ![]() в точке
в точке ![]() также имеет бесконечный разрыв второго
рода.
также имеет бесконечный разрыв второго
рода.
2. Функция ![]() имеет в точке
имеет в точке ![]() устранимый
разрыв,
устранимый
разрыв, ![]() - разрыв второго рода (бесконечный).
- разрыв второго рода (бесконечный).
3. Если ![]() , то
, то ![]() ; если
; если ![]() , то
, то ![]() . В
точке
. В
точке ![]() разрыв первого рода типа скачок.
разрыв первого рода типа скачок.
4. В точке ![]() разрыв второго рода. Предел
разрыв второго рода. Предел 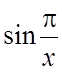 не существует при
не существует при ![]() .
.
5. Функция имеет
три точки разрыва. При ![]() - разрыв устранимый, при
- разрыв устранимый, при ![]() - разрыв второго рода (бесконечный).
- разрыв второго рода (бесконечный).
6. При ![]() - разрыв второго рода (бесконечный).
- разрыв второго рода (бесконечный).
7. При ![]() - разрывы второго рода (бесконечные).
- разрывы второго рода (бесконечные).
8. При ![]() и
и ![]() -
разрывы второго рода (бесконечные).
-
разрывы второго рода (бесконечные).
9. Нет. Если ![]() справа, то
справа, то ![]() , если
, если ![]() слева, то
слева, то ![]() .
.
10. Нет. Если ![]() справа, то
справа, то ![]() , если
, если ![]() слева, то
слева, то ![]() .
.
11. При ![]() - разрыв первого рода (скачок).
- разрыв первого рода (скачок).
12. При ![]() - разрыв первого рода (скачок), в точке
- разрыв первого рода (скачок), в точке ![]() функция непрерывна.
функция непрерывна.
13. В точке ![]() функция непрерывна, в точке
функция непрерывна, в точке ![]() - разрыв первого рода (скачок).
- разрыв первого рода (скачок).
14. В точке ![]() - разрыв первого рода (скачок), в точке
- разрыв первого рода (скачок), в точке ![]() функция непрерывна.
функция непрерывна.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.