Метод бисекции. Теорема Больцано-Коши

Метод бисекции.

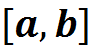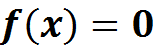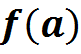Пуст на отрезке  расположен единственный корень  уравнения , а  и 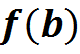 имеют разные знаки.

Положим = 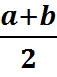и вычислим.

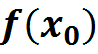Очевидно,  принадлежит тому из интервалов 

(a, 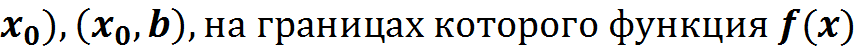 имеет разные знаки. В качестве  берём середину этого интервала и повторяем описанный процесс до тех пор пока на очередном шаге длина полученного интервала не станет меньше заданной точности .

Тогда за приближённое значение корня принимается середина этого интервала.

Формальная запись:

 

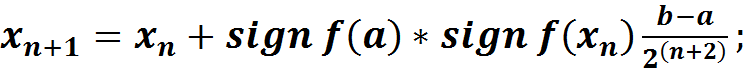
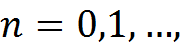
где .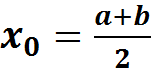

Теорема Больцано-Коши.

Пусть для непрерывной функции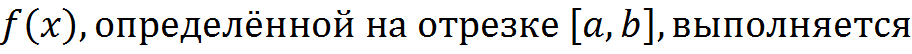

Неравенство .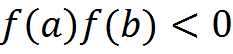

Тогда на интервале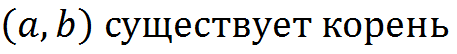

Уравнения 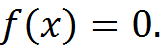 Если функция  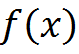монотонна на отрезке 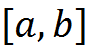, то этот корень единственный.

Описание программы.

Мы используем функцию 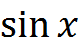, чтобы показать некоторые особенности программы.

Сначала программы проверяет, не являются ли границы, введенные пользователем корнями нашей функции. Если это так, то программа сразу же выводит ответ.

Далее программа смотрит знаки функции на концах отрезка. Если знаки одинаковы, то возможно корней на данном интервале нет.

Если знаки различны, то программа начинает делить отрезок пополам до заданной точности и выводит приближённое значение.

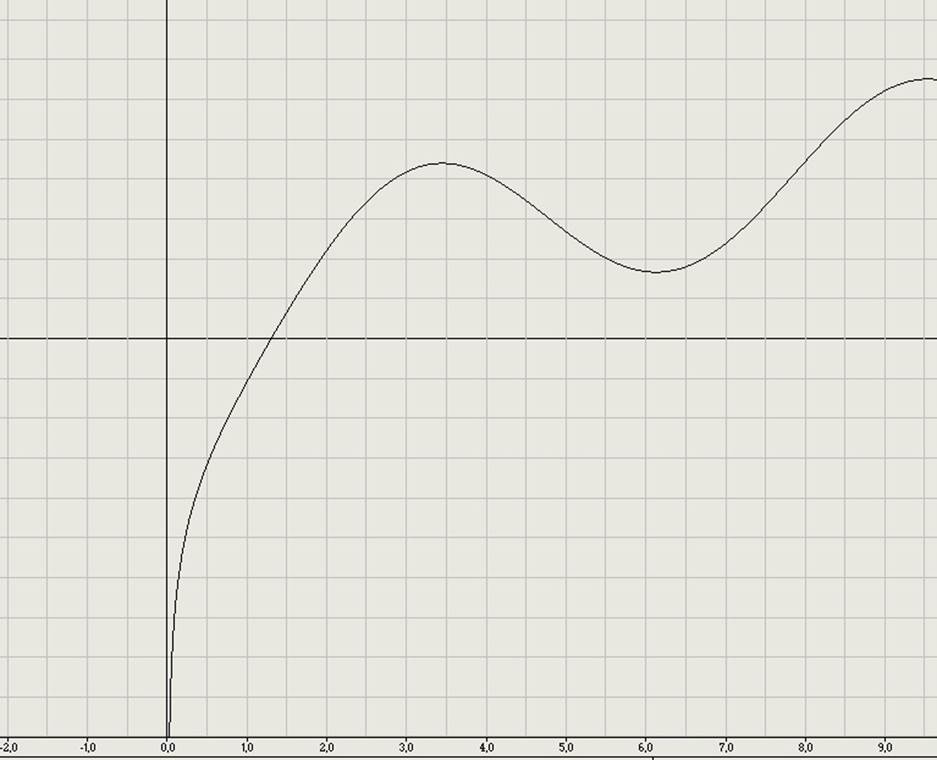
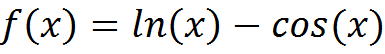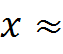Так же я тестировал программу на функции  где 1,303

Отрезок	Точность	Результат	Кол-во итераций
[0,2]	0.1	1.281250	5
[0,2]	0.01	1.300781	8
[0,2]	0.001	1.303223	11
[1.1,2.1]	0.1	1.318750	4