Построение кривой переходного процесса [1, с.168].
Дифференциальное уравнение системы для ошибки:
![]() .
.
Здесь g,f – задающее и возмущающее воздействия, р – оператор дифференцирования.
Решение линейного уравнения с постоянными коэффициентами:
![]() .
.
Здесь ![]() – общее решение однородного
уравнения
– общее решение однородного
уравнения ![]() (переходная составляющая), имеет, в
случае отсутствия нулевых и кратных корней, вид:
(переходная составляющая), имеет, в
случае отсутствия нулевых и кратных корней, вид:
![]() .
.
При наличии кратных корней:
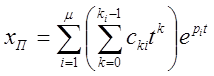 .
.
Здесь ![]() ,
, ![]() –
произвольные постоянные, определяемые начальными условиями,
–
произвольные постоянные, определяемые начальными условиями, ![]() – корни характеристического уравнения
– корни характеристического уравнения ![]() .
.
Частное, или вынужденное
решение ![]() определяется правой частью уравнения
движения. Оно соответствует некоторому установившемуся режиму после
затухания переходной составляющей
определяется правой частью уравнения
движения. Оно соответствует некоторому установившемуся режиму после
затухания переходной составляющей ![]() . Вид
членов
. Вид
членов ![]() и
и ![]() существенным
образом влияет на вид переходного процесса.
существенным
образом влияет на вид переходного процесса.
Для систем стабилизации
(![]() ) в качестве типовых используются
возмущающие воздействия в виде единичной ступенчатой функции
) в качестве типовых используются
возмущающие воздействия в виде единичной ступенчатой функции ![]() или единичной импульсной функции
или единичной импульсной функции ![]() . Для следящих систем в качестве
типовых используются задающие воздействий в виде единичной ступенчатой функции
. Для следящих систем в качестве
типовых используются задающие воздействий в виде единичной ступенчатой функции ![]() или линейно растущей функции
или линейно растущей функции ![]() .
.
Непосредственное решение дифференциального уравнения [1, с.171].
Пусть система автоматического регулирования описывается линейным дифференциальным уравнением:
![]() .
.
Для отыскания полного решения необходимо найти частное (вынужденное) решение этого неоднородного уравнения и определить корни характеристического уравнения, определяющие вид общего решение однородного уравнения:
![]() .
.
Далее входящие в общее решение произвольные постоянные определяются из начальных условий.
Для типового входного воздействия вида единичной ступенчатой функции решение исходного неоднородного уравнения может быть сведено к решению однородного уравнения путём перехода к другой переменной. За метим, что исходное уравнение для определения реакции системы на единичную функцию
![]()
замечательно тем, что 1(t) имеет разрыв первого рода при ![]() ,
поэтому правая часть содержит производные от разрывной функции. Процедура
изгнания производных от разрывной функции
,
поэтому правая часть содержит производные от разрывной функции. Процедура
изгнания производных от разрывной функции ![]() достаточно
сложная. Желающие могут найти её в [4, с.222].
достаточно
сложная. Желающие могут найти её в [4, с.222].
Единственным и достаточным в данном случае результатом указанной процедуры является совокупность начальных условий, которые и учитывают эффект правой части уравнения движения:
![]() ,
, ![]() , …,
, …, ![]() ,
,
…
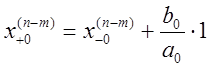 ,
,
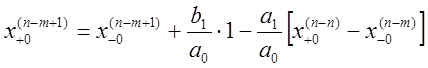 ,
,
…
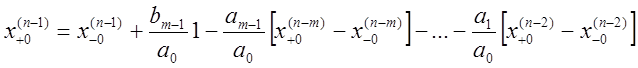 .
.
Итак, переходной процесс
определяется видом корней характеристического уравнения и начальными условиями,
учитывающими эффект правой части. Решение, содержащее произвольные постоянные,
дифференцируется ![]() раз. Используя начальные
условия, получают систему уравнений, откуда находятся эти постоянные.
раз. Используя начальные
условия, получают систему уравнений, откуда находятся эти постоянные.
Пример.
Рассмотрим уравнение движения груза на пружинке:
 .
.
Справа –
длящаяся одно мгновение бесконечно большая сила ![]() . Ясно,
что если первоначально, то есть до
. Ясно,
что если первоначально, то есть до ![]() , система находилась в
состоянии покоя, то сразу же после
, система находилась в
состоянии покоя, то сразу же после ![]() груз приобретёт
скорость
груз приобретёт
скорость ![]() .
.
В самом деле. В операторной форме уравнение движения имеет вид:
![]() .
.
Согласно выше изложенному формальному подходу, начальные условия:
![]() ,
, ![]() ,
, ![]() .
.
Применение преобразования Лапласа [1, c.177].
Применение преобразования Лапласа позволяет иным образом решить проблему нахождения начальных условий в присутствии возмущения.
Прямое и обратное преобразования
Лапласа (![]() )
)
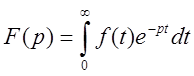 ,
, 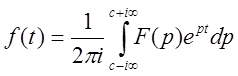 .
.
Здесь с – абсцисса абсолютной сходимости, выбирается так, чтобы
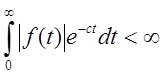 .
.
Применим преобразование Лапласа для решения дифференциального уравнения
![]() .
.
При переходе к изображениям уравнение приобретает вид:
![]() .
.
В ![]() включены
члены, содержащие начальные условия.
включены
члены, содержащие начальные условия.
Изображение искомой величины:
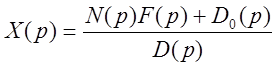 .
.
Как полагает автор [1], понятие начальных условий имеет различные трактовки в связи с тем, что строгое определение преобразования Лапласа
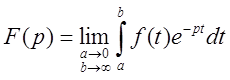
допускает, по его мнению, две трактовки.
Преобразование Лапласа по начальным условиям справа [1, c.180].
Если ![]() , то в изображении производной следует
брать начальные условия при
, то в изображении производной следует
брать начальные условия при ![]() :
:
![]() .
.
Но начальные условия справа
зависят от внешнего воздействия. Даже если система находилась в состоянии
покоя, начальные условия могут оказаться ненулевыми. Для их определения
придётся применить упомянутую выше непростую процедуру. Кроме того, если
возмущение ![]() имеет при
имеет при ![]() особенности
типа
особенности
типа ![]() -функции, то изображение самой функции и её
производных оказывается равным нулю:
-функции, то изображение самой функции и её
производных оказывается равным нулю:
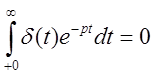 ,
, 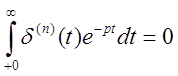 .
.
Преобразование Лапласа по начальным условиям слева [1, c.181].
Если ![]() , то в изображении производной следует
брать начальные условия при
, то в изображении производной следует
брать начальные условия при ![]() :
:
![]() .
.
Такие начальные условия называются предначальными. При нулевых предначальных условиях
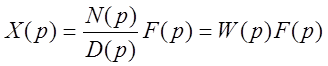 .
.
Изображения ![]() -функции и её производных:
-функции и её производных:
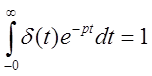 ,
, 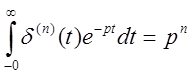 .
.
Влияние особенностей
![]() и её производных на изображение
и её производных на изображение ![]() в части начальных условий справа в этом
случае учитывается автоматически в самом изображении
в части начальных условий справа в этом
случае учитывается автоматически в самом изображении ![]() без
введения дополнительного члена
без
введения дополнительного члена ![]() при нулевых
предначальных условиях или без его изменения при ненулевых предначальных
условиях.
при нулевых
предначальных условиях или без его изменения при ненулевых предначальных
условиях.
Для отыскания оригинала по его изображению пользуются соответствующими таблицами.
Если изображение Лапласа имеет вид отношения двух полиномов
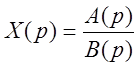 ,
,
можно воспользоваться теоремой разложения. При отсутствии нулевых корней знаменателя решение имеет вид:
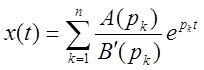 .
.
При наличии нулевого корня (![]() ):
):
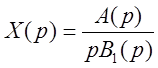 ,
, 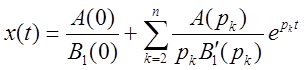 .
.
При наличии пары мнимых корней (![]() ,
,![]() )
)
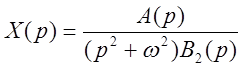 ,
, 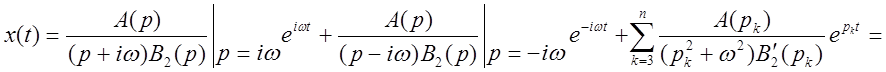
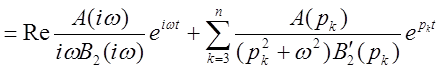 .
.
Иной подход к проблеме учёта начальных условий можно найти в [4]. Преобразование Лапласа производится по начальным условиям справа (напомним, что такой подход был отвергнут авторами монографии [1]).
Пример [4, c.501].
Уравнение движения:
![]() .
.
Начальные условия: ![]() ,
, ![]() ,
, ![]() .
.
Преобразование по Лапласу:
![]() .
.
Изображение решения:
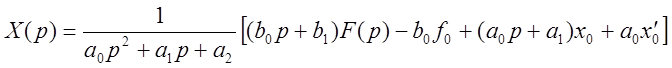 .
.
Левый множитель называется системной функцией. Правый множитель содержит возмущение и начальные условия и называется возбуждающей функцией.
Напомним, что в состав возбуждающей
функции входят правые начальные значения функций ![]() ,
,
![]() . И здесь появляется та же проблема с
. И здесь появляется та же проблема с ![]() -функциями.
-функциями.
Автор [4]
предлагает следующее: если функция ![]() разрывна, то следует
считать появляющиеся при её дифференцировании
разрывна, то следует
считать появляющиеся при её дифференцировании ![]() -функции
и их производные как преобразуемые по Лапласу лишь условно. В самом
деле, при формальном подходе оказывается, что
-функции
и их производные как преобразуемые по Лапласу лишь условно. В самом
деле, при формальном подходе оказывается, что ![]() .
.
Так, например, принято
считать, что ![]() . А формально:
. А формально:
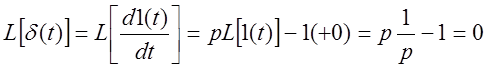 .
.
Получили неверный результат.
Чтобы поправить дело автор [4] предлагает в данном случае считать ![]() . Так что если
. Так что если ![]() , то
следует положить
, то
следует положить ![]() .
.
Рассмотрим снова уравнение движения груза на пружинке:

Справа – длящаяся одно мгновение
бесконечно большая сила ![]() . Ясно, что если
первоначально, то есть до
. Ясно, что если
первоначально, то есть до ![]() , система находилась в
состоянии покоя, то сразу же после
, система находилась в
состоянии покоя, то сразу же после ![]() груз приобретёт
скорость
груз приобретёт
скорость ![]() .
.
Определим ![]() следующим образом:
следующим образом:
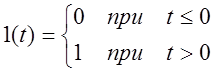 .
.
При этом ![]() -функция
и её производные расположатся справа от нуля. То есть система покоится
вплоть до
-функция
и её производные расположатся справа от нуля. То есть система покоится
вплоть до ![]() , а затем её толкают.
, а затем её толкают.
Преобразование Лапласа даёт:
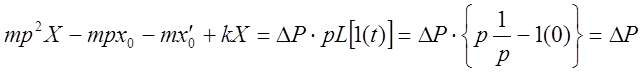 .
.
При собственных нулевых
начальных условиях ![]() ,
, ![]() :
:
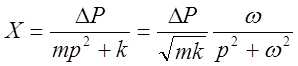 ,
, 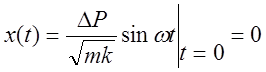 ,
, 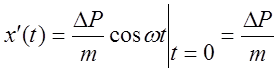 .
.
Здесь ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.