


Позиционные динамические звенья [1].
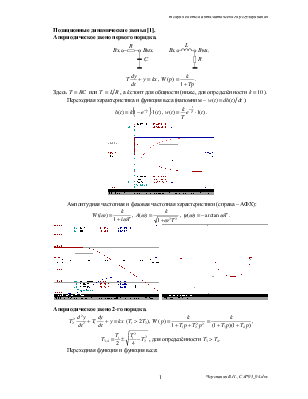
Апериодическое звено первого порядка.
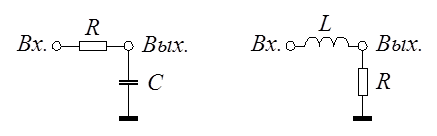
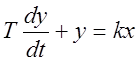 ,
, 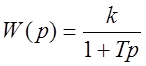 .
.
Здесь ![]() или
или ![]() , а k стоит
для общности (ниже, для определённости
, а k стоит
для общности (ниже, для определённости ![]() ).
).
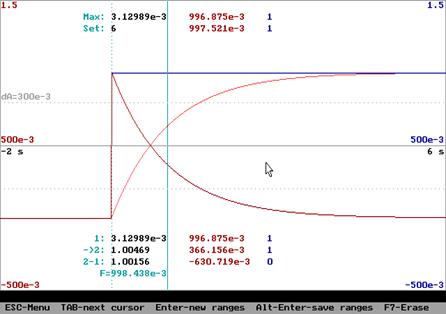
Переходная
характеристика и функция веса (напомним – ![]() ):
):
![]() ,
, 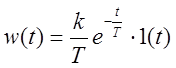 .
.
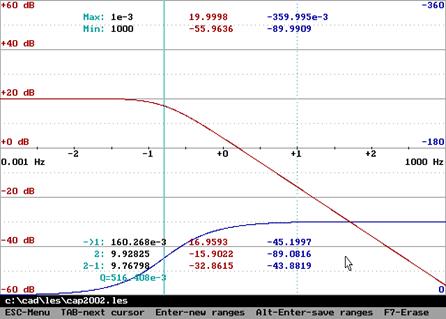
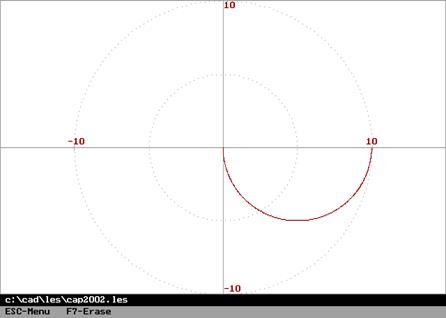
Амплитудная частотная и фазовая частотная характеристики (справа – АФХ):
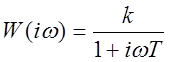 ,
, 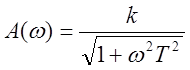 ,
, ![]() .
.
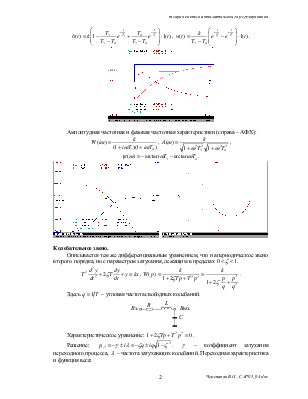
Апериодическое звено 2-го порядка.
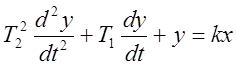 (
(![]() ),
), 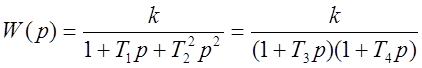 ,
,
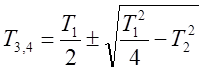 , для определённости
, для определённости ![]() .
.
Переходная функция и функция веса:
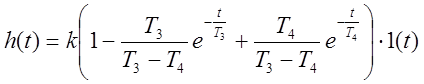 ,
, 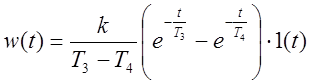 .
.
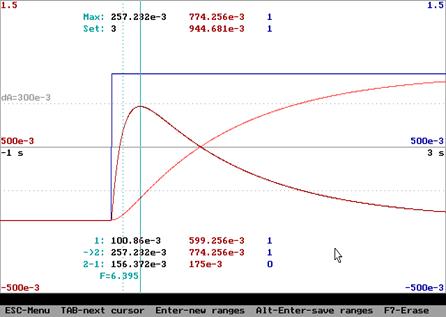
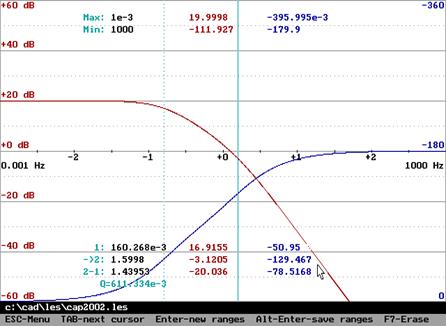
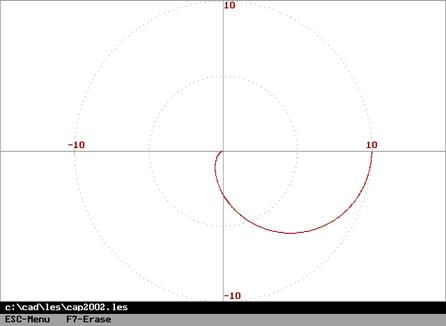
Амплитудная частотная и фазовая частотная характеристики (справа – АФХ):
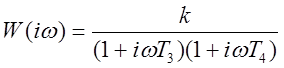 ,
, 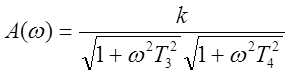 ,
, ![]() .
.
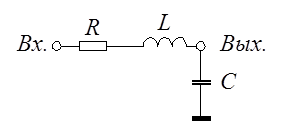
Колебательное звено.
Описывается тем
же дифференциальным уравнением, что и апериодическое звено второго порядка, но
с параметром затухания, лежащим в пределах ![]() .
.
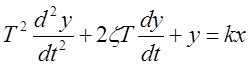 ,
, 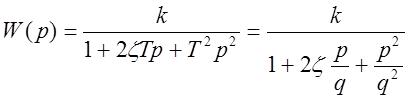 .
.
Здесь ![]() –
угловая частота свободных колебаний.
–
угловая частота свободных колебаний.
Характеристическое
уравнение: ![]() .
.
Решение: ![]() .
. ![]() –
коэффициент затухания переходного процесса,
–
коэффициент затухания переходного процесса, ![]() –
частота затухающих колебаний. Переходная характеристика и функция веса:
–
частота затухающих колебаний. Переходная характеристика и функция веса:
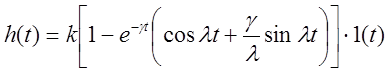 ,
, 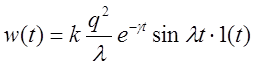
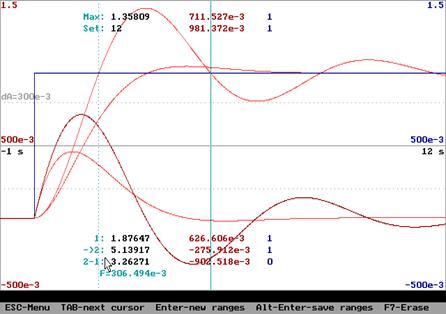
Амплитудная частотная и фазовая частотная характеристики (справа – АФХ):
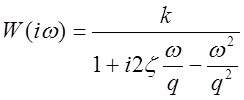 ,
, 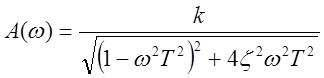 ,
, 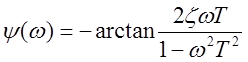 .
.
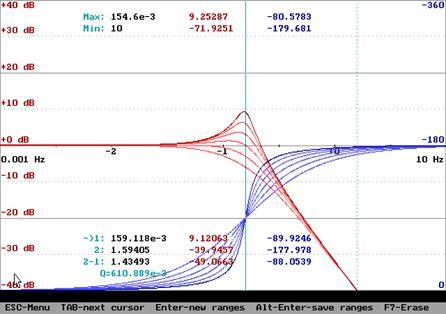
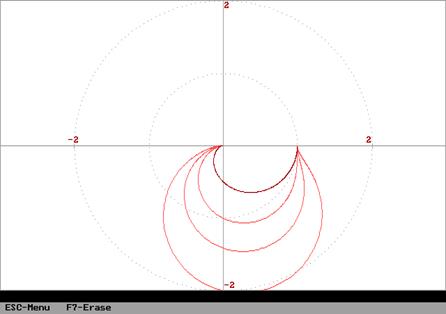
Амплитудная
частотная характеристика имеет пик при ![]() :
:
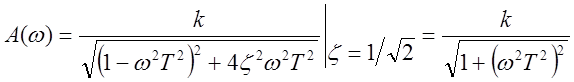
– характеристика Баттерворта.
Пик с
амплитудой 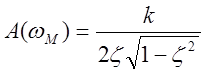 соответствует частоте
соответствует частоте ![]() .
.
Консервативное звено
является частным случаем колебательного при ![]() :
:
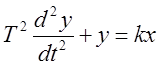 ,
, 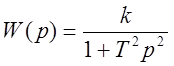 ,
,
Переходная функция и функция веса:
![]() ,
, ![]() .
.
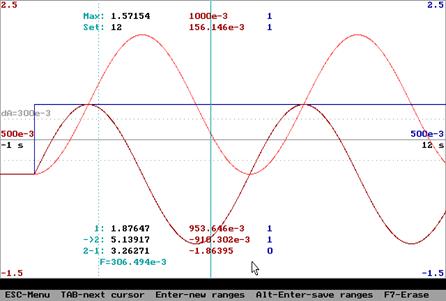
Амплитудная
частотная и фазовая частотная характеристики (![]() ):
):
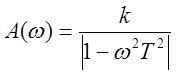 ,
, 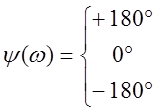 при
при 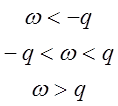 .
.
Интегрирующие звенья.
Идеальное интегрирующее звено.
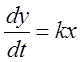 (
(![]() ),
), 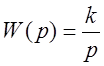 .
.
Таким звеном является операционный усилитель в режиме интегрирования:
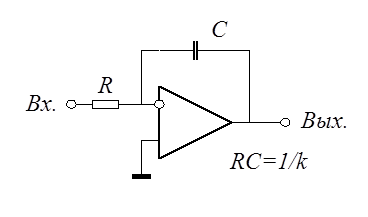
Переходная
характеристика и функция веса: ![]() ,
, ![]() .
.
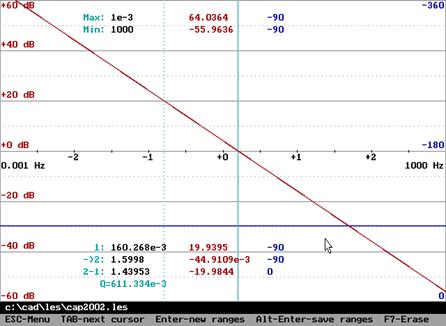
Амплитудная частотная и фазовая характеристики (справа – АФХ):
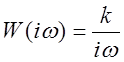 , частота среза
, частота среза ![]() ,
, 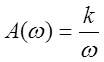 ,
, ![]() .
.
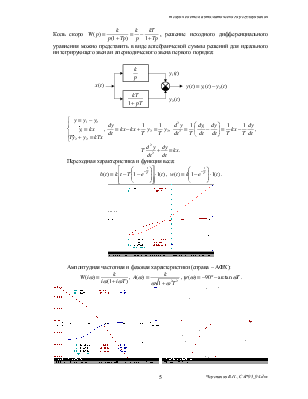
Интегрирующее звено с замедлением.
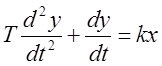 ,
, 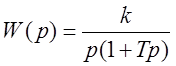 .
.
Коль скоро 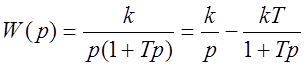 , решение исходного дифференциального
уравнения можно представить в виде алгебраической суммы решений для идеального
интегрирующего звена и апериодического звена первого порядка:
, решение исходного дифференциального
уравнения можно представить в виде алгебраической суммы решений для идеального
интегрирующего звена и апериодического звена первого порядка:
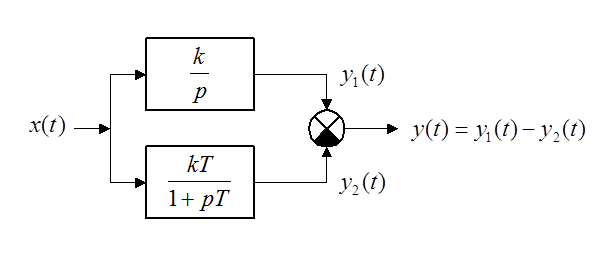
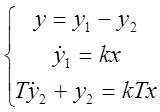 ,
, 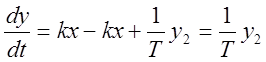 ,
, 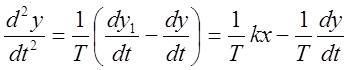 ,
,
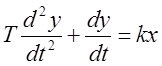 .
.
Переходная характеристика и функция веса:
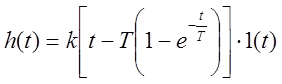 ,
, 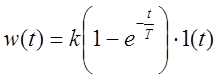 .
.
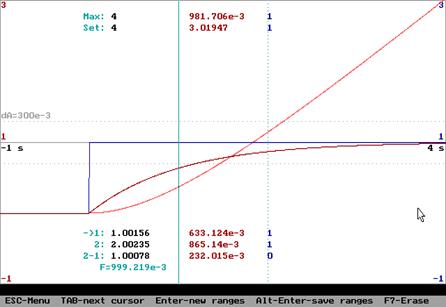
Амплитудная частотная и фазовая характеристики (справа – АФХ):
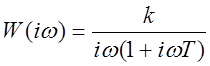 ,
, 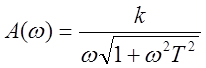 ,
, ![]() .
.
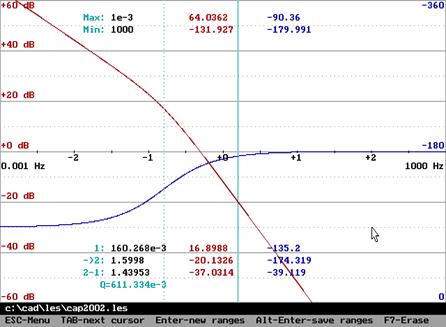
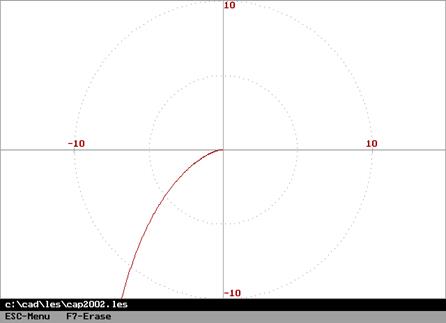
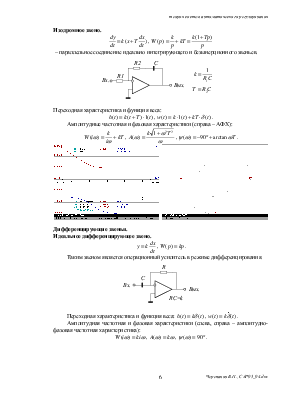
Изодромное звено.
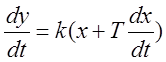 ,
, 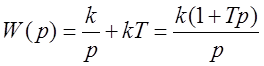
– параллельное соединение идеально интегрирующего и безынерционного звеньев.
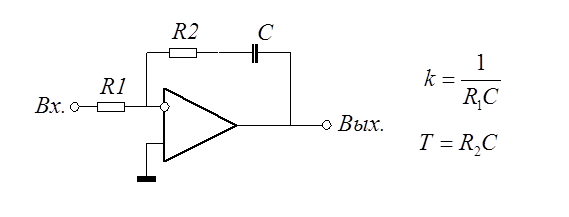
Переходная характеристика и функция веса:
![]() ,
, ![]() .
.
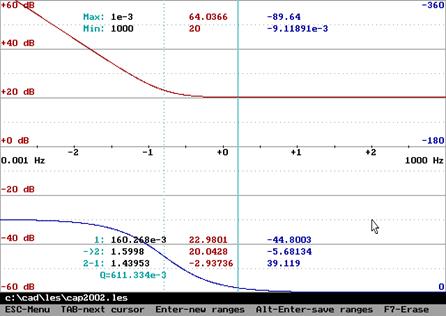
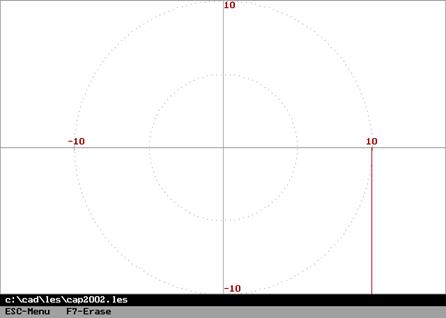
Амплитудные частотная и фазовая характеристики (справа – АФХ):
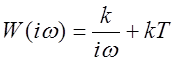 ,
, 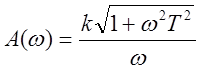 ,
, ![]() .
.
Дифференцирующие звенья.
Идеальное дифференцирующее звено.
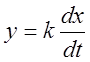 ,
, ![]() .
.
Таким звеном является операционный усилитель в режиме дифференцирования.
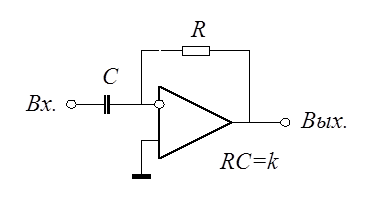
Переходная
характеристика и функция веса: ![]() ,
, ![]() .
.
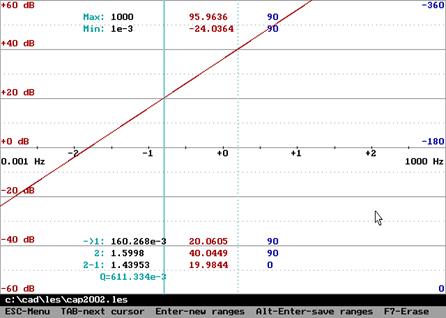
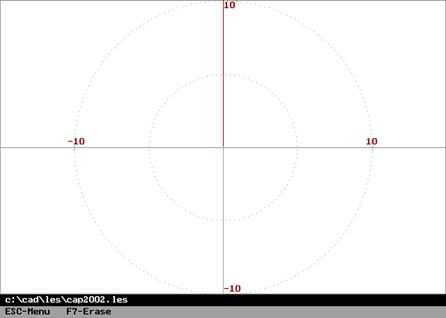
Амплитудная частотная и фазовая характеристики (слева, справа – амплитудно-фазовая частотная характеристика):
![]() ,
, ![]() ,
, ![]() .
.
Дифференцирующее звено с замедлением.
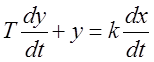 ,
, 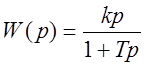 .
.
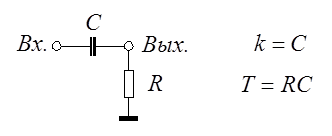
Переходная характеристика и функция веса:
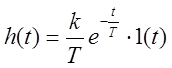 ,
, 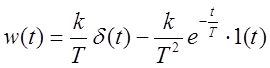 .
.
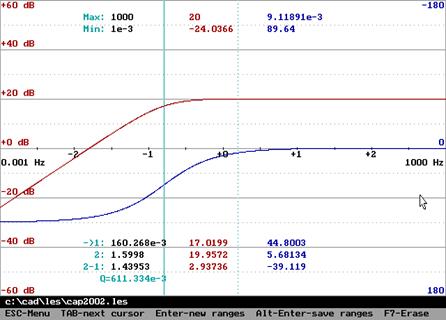
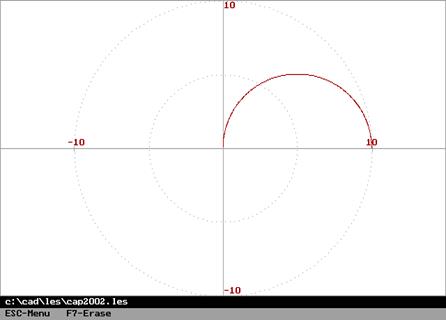
Амплитудная частотная и фазовая характеристики (слева, справа – амплитудно-фазовая частотная характеристика):
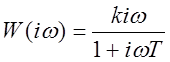 ,
, 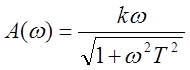 ,
, ![]() .
.
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.