Пленение излучения (Раздел 3.3. учебного пособия)

3.3. Пленение излучения

Из раздела 3.2 мы увидели, что на ширину линии излучения атомной (или молекулярной) системы существенно влияют процессы, происходящие в этой атомной системе. В частности, тепловые движения или столкновения приводят обычно к уширению линии. В данном разделе мы рассмотрим влияние эффектов взаимодействия излученного фотона с окружающими атомами, прежде чем он покинет объем, занимаемый системой атомов, то есть излучающей средой.

Будем предполагать, что излучающая cреда занимает слой, бесконечный в направлениях x и y и ограниченный вдоль z областью от z = 0 до z = . Задачу можно рассматривать, как одномерную с потоком фотонов, распространяющихся вдоль оси z.

Тогда уравнение баланса для плотности nw фотонов с частотой  [5]

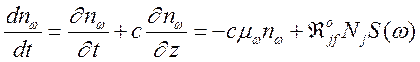                    (161)

можно переписать в виде

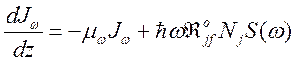.                          (162)

Здесь использовано, что задача стационарна 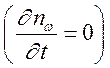 и приняты обозначения:  — интенсивность излучения фотонов с частотой  через единицу поверхности:

                                (163)

— коэффициент поглощения  или усиления  потока фотонов на единице пути;  и  — концентрация атомов на верхнем j и нижнем f энергетических уровнях.  — cечения поглощения и вынужденного излучения (см. раздел 1.6).

Величины сечений могут быть найдены из условия термодинамического равновесия излучения и атомов. Сечение  равно отношению вероятности индуцированного излучения в единицу времени, рассчитанной квантовомеханическим методом в разделе 3.1, к классической плотности потока фотонов.

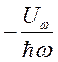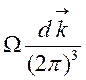Плотность потока фотонов, приходящаяся на единичный интервал частот , найдем из следующих условий. Энергия электромагнитного поля в объеме , в классическом приближении равна . С другой стороны, она равна произведению энергии фотона , среднего их числа , числа состояний  и  — числа состояний поляризации, то есть

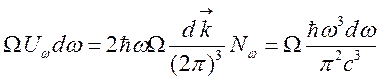.                       (164)

Следовательно

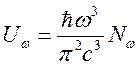.                                            (165)

Используя (153) имеем

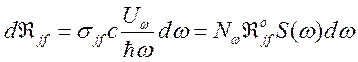,                        (166)

с учетом (165) для сечения вынужденного излучения получим

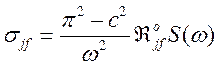.                                       (167)

Учитывая связь вероятности прямой и обратной реакции (42, 43), получим

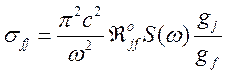                                     (168)

и

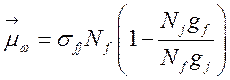,                                   (169)

где j,f — индексы верхнего и нижнего уровней атома,  — статвеса.

Предположим, что , то есть поглощение очень мало. Тогда из (162) для интенсивности излучения с единицы поверхности cреды получим

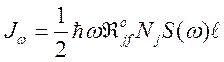.                                   (170)

Коэффициент 1/2 обусловлен наличием излучения через две границы z = 0 и z = . В этом случае регистрируемая ширина линии будет обусловлена процессами, определяющими условия излучения отдельного атома, т.е. эффектом Допплера и Лоренцовским профилем, формирование которых было рассмотрено ранее (см. разделы 3.1, 3.2).

В другом предельном случае  (предполагаем, что в среде присутствует поглощение, то есть , излучение свободно без поглощения выходит наружу только из пограничной области масштаба .

Тогда интенсивность спонтанного излучения в спектральном интервале вблизи центра (при максимуме поглощения) оказывается равнa

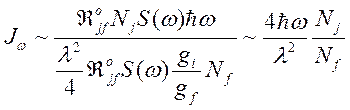,                         (171)

то есть не зависит от профиля линии излучения.

Следовательно в некотором спектральном интервале вблизи центра линии, для которого , интенсивность уменьшается по сравнению с (170) в . Необходимо отметить, что при различных  в пределах ширины линии значение  различно и, следовательно, изменяется и глубина области, из которой выходит излучение.

Среда считается тонкой для данной , если  и оптически “толстой”, если . При частоте, для которой , интенсивность излучения снова начинает определяться профилем линии .

Уменьшение интенсивности свечения в центре линии можно интерпретировать как уменьшение вероятности спонтанного излучения. Проинтегрировав (170) по всем частотам получим для “тонкого” слоя

                                       (172)

и для “толстого” слоя

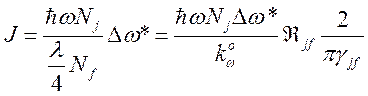.                   (173)

Сравнение (172) и (173) показывает, что

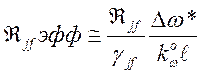,                                      (174)

где  — новая ширина линии, определяемая из условия ,  — коэффициент поглощения в центре линии и  — ширина невозмущенной линии.

Таким образом, если поглощение велико, то условие  может выполняться только на краю линии поглощения, профиль которой определяется . Следовательно,  будет существенно шире, чем линия излучения оптически “тонкой” среды.