Перезарядка. Резонансная перезарядка атома водорода (Глава 8 учебного пособия)

8. Перезарядка

8.1 Резонансная перезарядка атома водорода

Перезарядкой называется процесс обмена зарядом при столкновении двух частиц, т.е. реакция типа

                                        (8.1)

Обычно в процессе перезарядки происходит передача электрона. Резонансной считается перезарядка, когда сталкиваются две однотипные частицы. Рассмотрим обмен зарядом при столкновении протона с атомом водорода:

                                        (8.2)

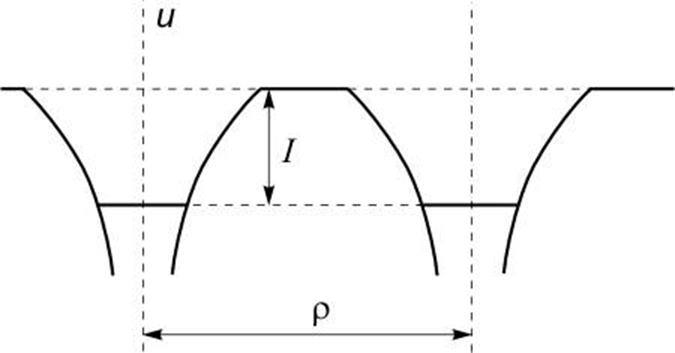
При энергиях сталкивающихся атомов, превышающих энергию связи, их движение можно считать прямолинейным. Если , то  — скорость движения ядер мала по сравнению с  — средней скоростью электрона в атоме. Сечение перезарядки в этом случае велико и определяется прицельным параметром , превышающим характерный размер атома  [10]. Чтобы перезарядиться, электрону необходимо пройти через потенциальный барьер, высота которого равна I — потенциалу ионизации (рис. 7).

К моменту наименьшего сближения вероятность электрона совершить переход за единицу времени равна

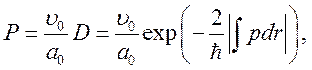                                   (8.3)

где , a  — число ударов о стенку электрона в единицу времени. Экспонента описывает вероятность проникновения через потенциальный барьер, вычисленную в квазиклассическом приближении. Домножая Р на время пролета, получим вероятность перезарядки:

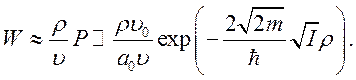                                        (8.4)

При малых , W > 1, что означает, что электрон может несколько раз перейти от одного протона к другому, т.е. вероятность перезарядки . Характерный масштаб можно, найти, приняв , т.е.

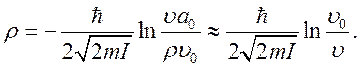                                  (8.5)

Под логарифмом можно принять  при  Тогда сечение

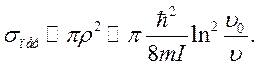                                      (8.6)

Если учесть, что  и , то получим

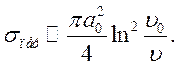                                             (8.7)

8.2. Нерезонансная перезарядка атома водорода на многозарядном ионе

Взаимодействие электрона с протоном и многозарядным ионом описывается потенциалом

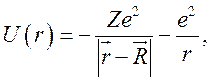                                            (8.8)

где R — межъядерное расстояние и r — расстояние от протона (рис. 8).

Вероятность перезарядки в единицу времени пропорциональна вероятности прохождения через потенциальный барьер

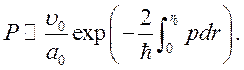                                        (8.9)

где и  — энергия связи электрона вблизи протона. Из (8.8) получим

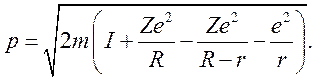                                 (8.10)

Считая  для p получим

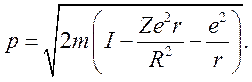
Поле протона слабо влияет на форму потенциального барьера, поэтому им можно пренебречь. Тогда для Р получим

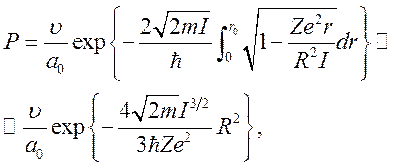                           (8.11)

где .

Учитывая, что , домножая P на время пролета и считая , получим для вероятности перезарядки

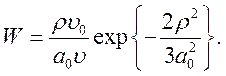                                        (8.12)

Аналогично (8.5) для нахождения  полагаем W~1:

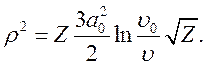
Сечение перезарядки равно

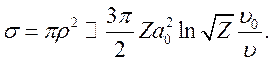                                   (8.13)

Используемое приближение называется распадной моделью. Расчет сечения перезарядки фактически свелся к вычислению вероятности распада атома водорода в электрическом поле ядра.

В случае захвата электрона многозарядным ионом из соображений простого резонанса внутренней энергии непосредственно следует, что захват происходит преимущественно в состояние с главным квантовым числом .

Действительно, энергия связи электрона при бесконечно большом расстоянии между продуктами определяется выражением , где . После взаимодействии энергия электрона в поле заряда Z равна , где n — главное квантовое число. Из получим n=Z. Если считать, что перезарядка происходит на конечном расстоянии , то появляется дополнительная энергия взаимодействия ионов: протона и иона с заряда (Z — 1). Тогда

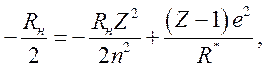                                   (8.14)

где — расстояние между протоном и ионом.

Предположим, что перезарядка происходит, когда притяжение электрона к иону сравнимо с притяжением к протону. Тогда или . В действительности перезарядка за счет туннелирования может проходить на несколько больших расстояниях , где . Подставляя  в (8.14) и используя  получим

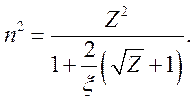                                        (8.15)

При  имеем . Эмпирическая зависимость .