
· Перезарядкой называется процесс обмена электроном при столкновении двух частиц (как правило, между ионом и атомом), т.е. реакция типа
![]() .
.
· Резонансной считается перезарядка, если внутренняя энергия взаимодействующих частиц не изменяется. Это реализуется, например, когда сталкиваются две однотипные частицы.
· Вероятность перезарядки определяется ее эффективным поперечным сечением, sпер.
· При энергии сталкивающихся атомов, Е, большей потенциальной энергии взаимодействия, их движение можно считать прямолинейным. Сечение перезарядки в этом случае определяется прицельным параметром r, меньшем размера атома а0.
Постановка задачи
|
![]()
|
|
|

|
|
|
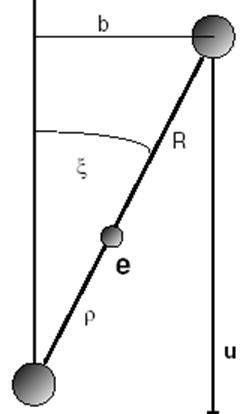
Рис.1. Геометрия взаимодействия атомных частиц при перезарядке
![]() .
.
1.
Пусть  кэВ,
тогда
кэВ,
тогда ![]() <
< ![]() , можно ожидать что sпер будет велико
, можно ожидать что sпер будет велико
![]()
2.
Для перезарядки электрону
необходимо пройти через потенциальный барьер, равный потенциалу ионизации ![]() .
.
![]()
![]()
![]()
![]()
|
|
|||
|
|||
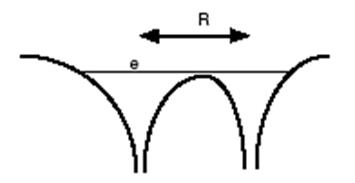
Рис.2.
Распределение потенциала при резонансной перезарядке
протона на атоме водорода
![]()
3. Вероятность совершить электрону переход от атома к протону за единицу времени равна:
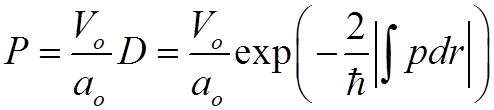 ,
,
где
D – коэффициент прохождения через потенциальный барьер;
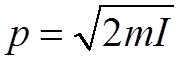 ; а
; а 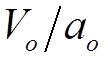 - число
ударов о потенциальный барьер электрона в единицу времени.
- число
ударов о потенциальный барьер электрона в единицу времени.
4.
Домножая Рна время пролета 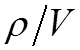 ,
получим вероятность перезарядки
,
получим вероятность перезарядки
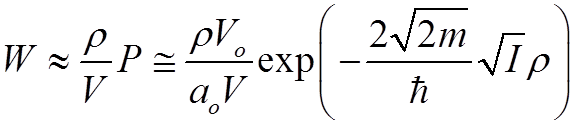 .
.
Видно,
что при малых ![]() , W может быть
формально >1. Это означает, что электрон может несколько раз
перейти от одного протона к другому, т.е. вероятность перезарядки
, W может быть
формально >1. Это означает, что электрон может несколько раз
перейти от одного протона к другому, т.е. вероятность перезарядки ![]() /2 (только один переход электрона от атома
водорода к протону).
/2 (только один переход электрона от атома
водорода к протону).
![]()
5.
Характерный масштаб ![]() (для определения сечения) можно найти,
приняв W~1 , т.е.
(для определения сечения) можно найти,
приняв W~1 , т.е.
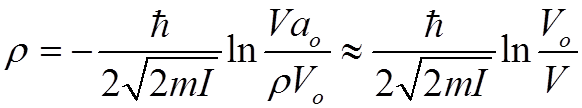 .
.
![]()
6.
Приняв 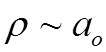 при
при  , для сечения перезарядки получим
, для сечения перезарядки получим
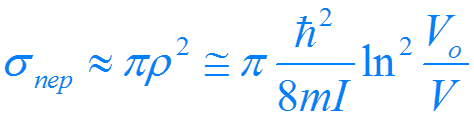 .
.
![]()
7.
С учетом того, что 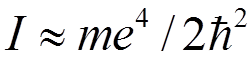 и
и 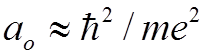 ,
получим окончательно
,
получим окончательно
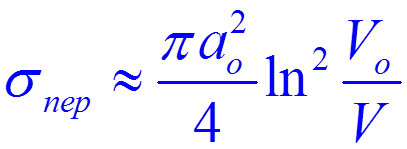 .
.
Постановка задачи
|
|
![]()
![]()
|
|



|
![]()
|
|
![]()
![]()
|
|
Рис.2. Распределение потенциала при перезарядке водорода на многозарядном ионе
![]()
1. Взаимодействие электрона с протоном и многозарядным ионом описывается потенциалом
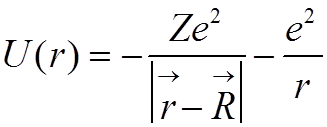 ,
,
где R - межядерное расстояние и r - расстояние от протона.
2. Вероятность перезарядки в единицу времени пропорциональна вероятности прохождения через потенциальный барьер
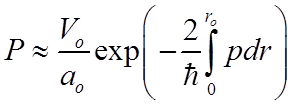 ,
,
где
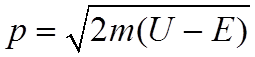 и
и 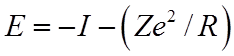 -
энергия связи электрона вблизи протона.
-
энергия связи электрона вблизи протона.
![]()
3. Определение импульса электрона
Используя зависимость для U, представим выражение для импульса в виде
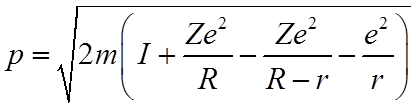 .
.
Далее: (1) считая r<<R и (2) что поле протона слабо влияет на форму потенциального барьера, получим
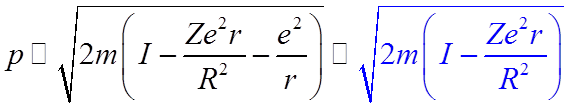 .
.
![]()
4. Откуда вероятность прохождения электрона через барьер
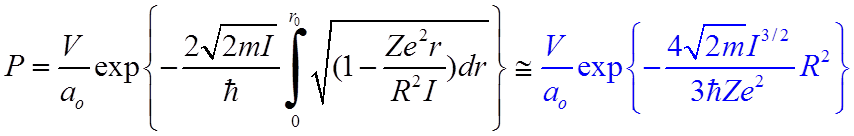 ,
,
где
![]() .
.
5.
Учитывая, что ![]() , и домножая P на время пролета
, и домножая P на время пролета ![]() и считая
и считая ![]() ,
получим для вероятности перезарядки
,
получим для вероятности перезарядки
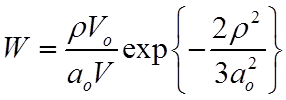 .
.
![]()
6. Полагая W ~ 1 , находим квадрат прицельного параметра
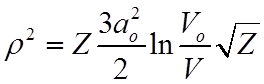 .
.
![]()
7. Откуда сечение перезарядки
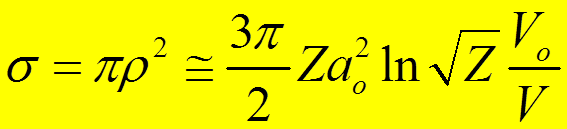 .
.
Используемое приближение называется распадной моделью (распад атома водорода в электрическом поле ядра).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.