Определение главного квантового числа захваченного электрона
1). В случае захвата электрона многозарядным ионом
захват происходит преимущественно в состояние с главным квантовым числом ![]() . Действительно, энергия связи электрона
при бесконечно большом расстоянии между продуктами определяется выражением
. Действительно, энергия связи электрона
при бесконечно большом расстоянии между продуктами определяется выражением
![]() ,
,
где ![]() –
постоянная Ридберга
–
постоянная Ридберга
![]()
2). После взаимодействия энергия электрона в поле заряда Z будет равна
![]() .
.
Учитывая,
что ![]() получим
получим
n = Z.
Однако необходимо учитывать того, что перезарядка происходит на конечном расстоянии R между протоном и ионом, необходимо учесть дополнительную энергию взаимодействия ионов: протона и иона с зарядом (Z- 1). Тогда
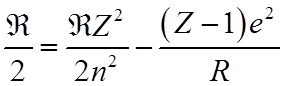 . (****)
. (****)
![]()
Предположим, что перезарядка происходит, когда притяжение электрона к иону сравнимо с притяжением к протону. Тогда
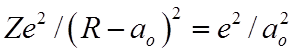 или
или 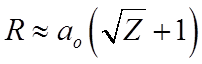 .
.
В действительности, перезарядка за счет туннелирования может проходить на несколько больших расстояниях
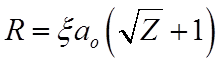 , где
, где ![]() .
.
Используя
![]() , из (*****) получим
, из (*****) получим
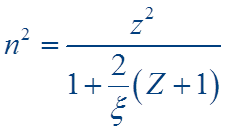 .
.
При
![]() имеем
имеем ![]() .
Эмпирическая зависимость
.
Эмпирическая зависимость ![]() .
.
 |
· Столкновения носителей зарядов противоположного знака, двигающихся в газе, которые приводят к их взаимной нейтрализации, называются рекомбинацией.
· Коэффициент рекомбинации, ![]() определяется как число
определяется как число ![]() актов рекомбинации в единице объема
за единицу времени, деленное на произведение плотностей носителей
заряда.
актов рекомбинации в единице объема
за единицу времени, деленное на произведение плотностей носителей
заряда.
![]() .
.
В простой двухкомпонентной системе обычно выполняется условие
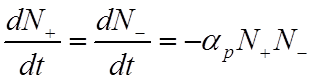 .
.
![]()
Коэффициент
рекомбинации связан с сечением рекомбинации ![]() соотношением
соотношением
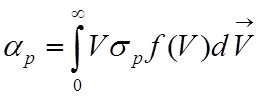 ,
,
которое
приближенно можно записать в виде ![]() , где V -
средняя тепловая скорость.
, где V -
средняя тепловая скорость.
![]()
Предположив
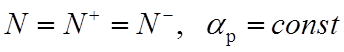 , а также что
, а также что ![]() при t=0, получим
при t=0, получим
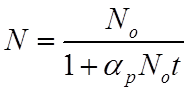 .
.
Если
в системе имеется источник ионизации Q и начальная плотность заряженных
частиц ![]() , то
, то
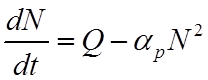 ,
,
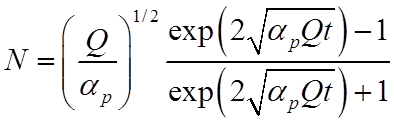 .
.
Равновесное
значение плотности ионов 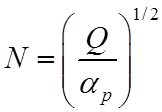 .
.
![]()
Трехчастичная рекомбинация
![]()
В соответствии с теорией Томсона две частицы могут соединиться , если их полная относительная энергия станет отрицательной, т.е. кинетическая энергия
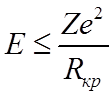 .
.
При столкновении частиц это невозможно.
Однако, если два электрона сталкиваются между собой на расстоянии Rкр от иона и энергия одного из электронов удовлетворяет данному условию, то он может быть захвачен ионом.
Полное
число столкновений электронов с другими электронами равно ![]() , где
, где ![]() -
средняя частота столкновений электронов.
-
средняя частота столкновений электронов.
Вероятность нахождения иона на критическом расстоянии Rкр равна
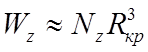 .
.
Количество ионов, рекомбинирующих в единице объема в единицу времени, равно
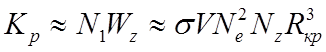 .
.
Здесь
![]() - сечение столкновения электронов, при
котором одной из частиц передается энергия порядка средней кинетической энергии
электронов Е .
- сечение столкновения электронов, при
котором одной из частиц передается энергия порядка средней кинетической энергии
электронов Е .
Полагая
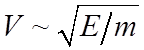 и считая сечение передачи энергии кулоновским
и считая сечение передачи энергии кулоновским
![]() , получим
, получим
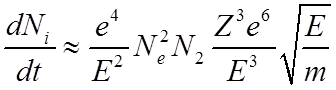 ,
,
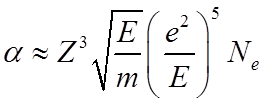 .
.
Точное выражение
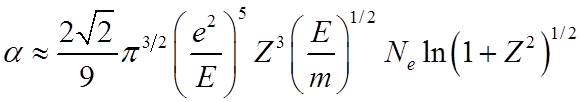 .
.
Радиационная рекомбинация (фоторекомбинация)
Определим сечение фоторекомбинации медленного электрона и иона с образованием сильно возбужденного атома.
Интенсивность дипольного излучения
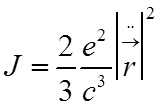 , где
, где ![]() - ускорение частицы.
- ускорение частицы.
Траектория,
дающая основной вклад в рекомбинацию, сильно искривлена. Пусть ![]() - расстояние наименьшего сближения, при
котором кинетическая энергия частицы равна
- расстояние наименьшего сближения, при
котором кинетическая энергия частицы равна
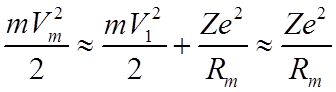 .
.
Пусть
![]() - прицельный параметр. Из закона
сохранения импульса получим
- прицельный параметр. Из закона
сохранения импульса получим
![]() .
.
Ускорение
электрона в точке ![]() равно
равно
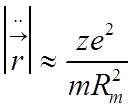 .
.
Для интенсивности дипольного излучения получим
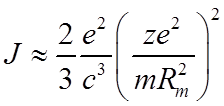 .
.
Вероятность столкновения с заданным прицельным параметром
![]() .
.
Полная излучаемая энергия
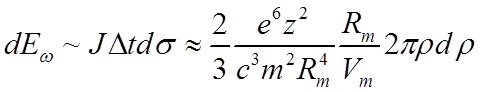 .
.
Используя закон сохранения импульса и выражение для кинетической энергии частицы, получим
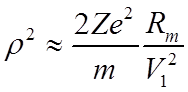 или
или 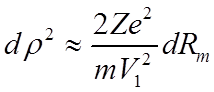 .
.
Основная излучаемая частота
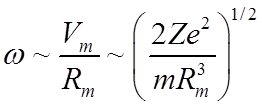 или
или 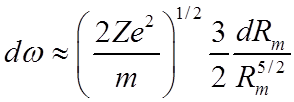 .
.
В результате получим
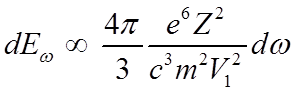 .
.
Излучаемая энергия связана с сечением рекомбинации
![]() .
.
Сравнивая два последних выражения, получим
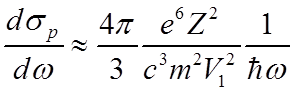 .
.
При этом должно выполняться
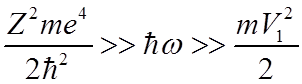 .
.
Учитывая,
что ![]() , то
, то 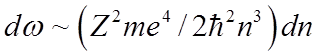 .
.
При
![]() получим
получим 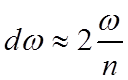 .
.
Здесь n - главное квантовое число уровня, на который попадает рекомбинирующий электрон.
Окончательное выражение для сечения рекомбинации (формула Крамерса):
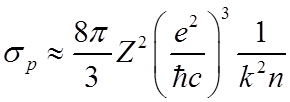 , где
, где ![]() .
.
Полное
сечение рекомбинации определяется суммированием по n ряда 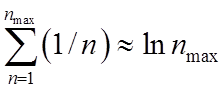 , где
, где ![]() определяется
условием, что при переходе на него излучается фотон с энергией
определяется
условием, что при переходе на него излучается фотон с энергией
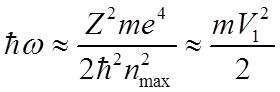 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.