Передаточные функции систем автоматического регулирования

Передаточные функции систем автоматического регулирования [1].

Замкнутая система автоматического регулирования:

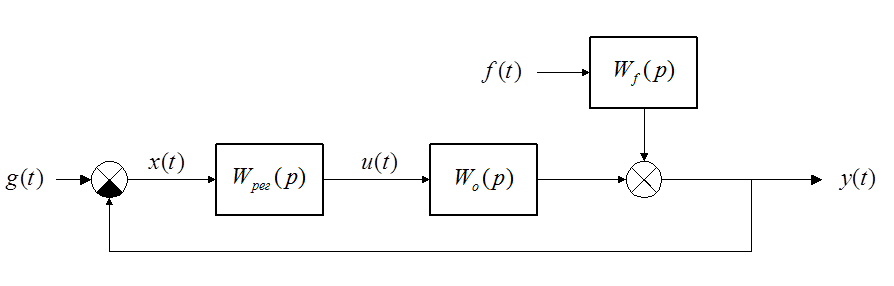
Здесь сам объект регулирования представлен передаточной функцией , определяемой видом дифференциального уравнения, описывающего динамику объекта регулирования (заданная функция). На его вход поступает управляющее воздействие

.

Здесь  – сигнал ошибки,  – задающее воздействие,  – регулируемая величина,  – передаточная функция регулятора (предмет разработки). Регулируемая величина определяется выражением:

.

Здесь  – передаточная функция объекта регулирования по возмущению .

С учётом вида управляющего воздействия:

.

Здесь  – передаточная функция по ошибке, она же – передаточная функция разомкнутой системы.

Уравнение замыкания

.

В результате для регулируемой величины:

.

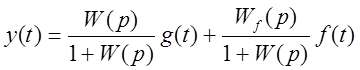Для ошибки:

.

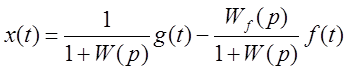Передаточная функция замкнутой системы и передаточная функция замкнутой системы по ошибке:

, .

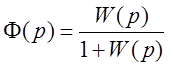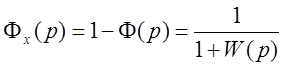Ведение автоматического регулирования уменьшает отклонение регулируемой величины под влиянием возмущений в  раз.

Законы регулирования.

Закон регулирования – зависимость управляющего воздействия от ошибки , задающего воздействия  и возмущения :

.

В общем случае это нелинейная функция x, u, f, а так же их производных и интегралов по времени. Обычно же она имеет вид:

.

Первое слагаемое соответствует регулированию по отклонению (принцип Ползунова-Уатта), второе и третье – регулированию по внешнему воздействию (принцип Понселе).

          Линейный закон регулирования по отклонению может иметь следующий вид:

.

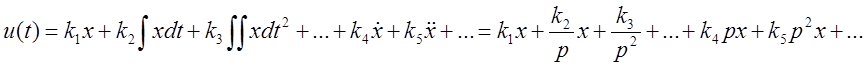Пропорциональное регулирование.

          Пусть регулируемый объект – звено статического типа: , или является таковым в установившемся состоянии (при ).

          Управляющее воздействие:

.

Передаточная функция разомкнутой системы:

 

 – общий коэффициент усиления разомкнутой системы.

          При постоянном задающем воздействии  установившаяся ошибка, называемая в данном случае статической ошибкой

.

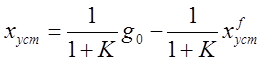Установившиеся ошибки по регулированию и возмущению уменьшились в  раз. Коль скоро они не равны нулю, регулирование называется статическим.

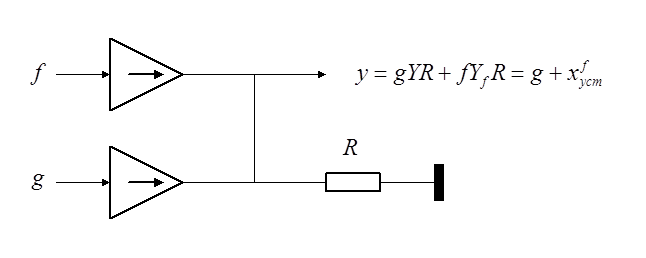
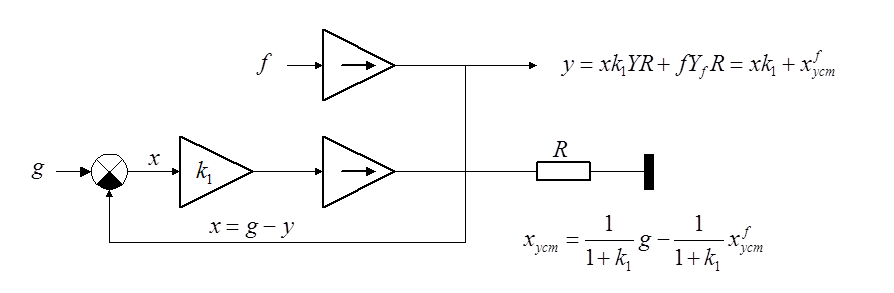
Пример.

Управляемые напряжением генераторы тока сигнала и помехи работают на общую нагрузку. В идеале  (при ).

Интегральное регулирование.

          Пусть регулируемый объект – звено статического типа: , или является таковым в установившемся состоянии (при ).

          Управляющее воздействие:

.

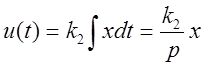Передаточная функция разомкнутой системы:

 

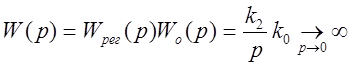
Первая составляющая ошибки при  обращается в нуль, т.е. система является астатической по отношению к управляющему воздействию. Что касается второй составляющей, то следует найти предел

,

который может быть как равным нулю, так и отличным от нуля.

          Регулирование может осуществляться и по второму интегралу от ошибки по времени:

.

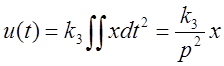В этом случае имеет место астатизм второго порядка. Ошибка, определяемая задающим воздействием, будет равна нулю не только при , но и при .

          Повышение порядка астатизма приводит к увеличению установившейся точности системы регулирования, но снижает её быстродействие. Кроме того, усугубляется проблема устойчивости.

Изодромное регулирование.

          Управляющее воздействие:

.

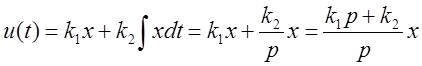Изодромное регулирование сочетает в себе точность интегрального регулирования с быстродействием пропорционального регулирования. В первый момент работает пропорциональное регулирование, с течением времени – интегральное.

Регулирование по производным.

          Управляющее воздействие:

.

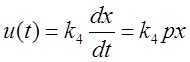Самостоятельного значения не имеет, так как в установившемся состоянии производная от ошибки равна нулю. Тем не менее, может играть большую роль в динамике – повышается быстродействие. Так, часто используется изодромное регулирование с добавлением первой производной:

.

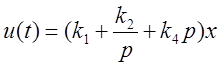Именно такой способ регулирования применён в системе стабилизации радиального положения пучка на протонном синхротроне ТРАПП (ИЯФ).