Основные виды прямолинейного движения точки. Криволинейное движение

§3.3 Основные виды прямолинейного движения точки. Криволинейное движение.

            Дифференциальное уравнение прямолинейного движения точки вдоль оси Ох имеет вид:

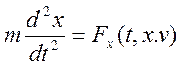
если рассматривается случай зависимости силы только от времени, координаты и скорости.  Начальные условия задаются в форме: t=0; x=x₀, v_x=v₀.

            Наиболее важные случаи прямолинейного движения точки получаются тогда, когда сила постоянна или она зависит только от времени, координаты х, или от скорости v. Если сила постоянна, то имеем случай равнопеременного движения, то есть движения с постоянным ускорением. Сила зависит от времени обычно, когда ее изменяют путем прямого регулирования. Силу, зависящую от координаты, создает сжатая пружина или центр тяготения. Силы, зависящие от скорости, чаще всего являются силами сопротивления.

Пример 1.

            Точка массы m движется под действием постоянной силы F с начальной скоростью v₀. (t=0, x=0, v_x=v₀)

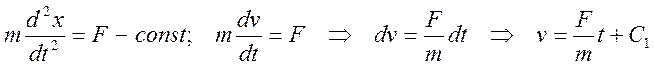
            используя начальные условия получаем С₁=v₀

 

 

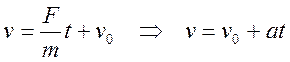
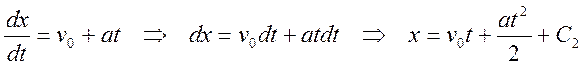
из начальных условий определяем С₂=0 и в результате закон движения точки имеет вид: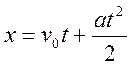

Пример 2.

            Точка массы m движется из начального положения покоя по действием переменной силы F=kSinwt. (начальные условия - t=0, x=0, v_x=0)

Из начальных условий определим

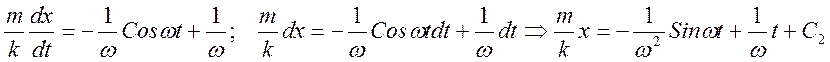 (t=0 àC₂=0)

Получаем, что тело будет двигаться равномерно с постоянной скоростью вправо и на это движение будет накладываться периодическое "модулирующее" движение. Заметим, что составляющей "дрейфа" не было бы, если бы начальные условия имели вид:

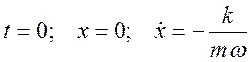
Пример 3.

            Точка массы m падает вертикально вниз без начальной скорости под действием силы тяжести, испытывая силу сопротивления воздуха R=kmv², где k-постоянная положительная величина. Найти уравнение движения точки.

Имеем ; (начальные условия - t=0, x=0, vx=0) Скорость в этом случае можно определить в зависимости от времени или от координаты, используя подстановки Последняя подстановка позволяет исключить из дифференциального уравнения время при определении скорости.

            Используя первую подстановку получаем дифференциальное уравнение:

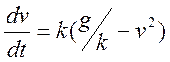
Разделяя переменные и беря интегралы от обеих частей имеем:

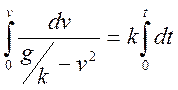
            Для того, чтобы не искать дополнительно произвольную постоянную, интегралы возьмем определенные, сохраняя верхний предел переменным для последующего интегрирования, а для нижних пределов используем начальные условия.

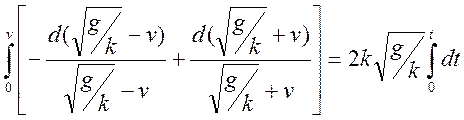
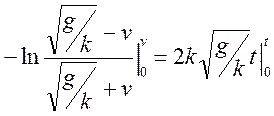 то есть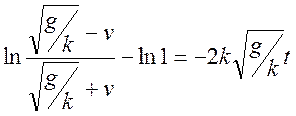

Потенциируя и решая относительно v, имеем:

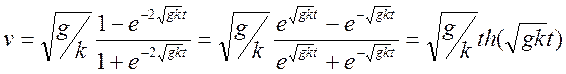
Переходя к пределу при  получаем

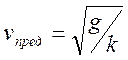
            Для нахождения закона движения теперь имеем: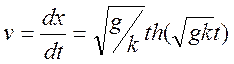

Отсюда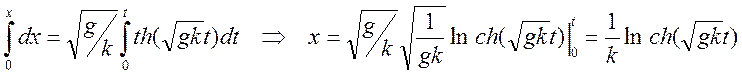

Пример 4.

            Точка массы m брошена вертикально вверх с поверхности земли с начальной скоростью v₀ и движется под действием силы тяготения

Начальные условия: t=0. x=R3, v=v0 Имеем дифференциальное уравнение:

Используя подстановку 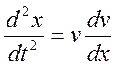 получаем уравнение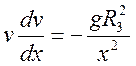

Разделяем переменные и берем интегралы:

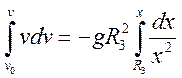 или 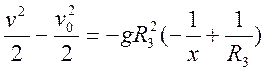, откуда

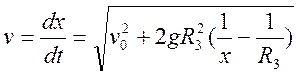 (3.3.1)

для определения x_max (максимальная высота подъема), положим v=0, тогда

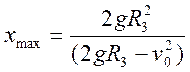 и при ,

это выполняется для v₀=11.2 км/с (вторая космическая скорость)

            Полученную зависимость (3.3.1.) скорости точки от высоты подъема можно использовать для определения закона движения ( x=f(t) ), разделив еще раз переменные и проведя интегрирование.

Пример 5 (криволинейное движение точки).

            Для случая криволинейного движения точки мы имеем два дифференциальных уравнения:

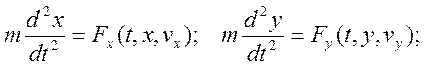
Рассмотрим движение точки массы m, входящей в воду под углом a с начальной скоростью v₀. В воде на точку действует сила сопротивления, пропорциональная скорости: , начальные условия задачи: t=0, x₀=0, y₀=0, v_x0=v₀Cosa, v_y0=v₀Sina.

Для оси х имеем  или

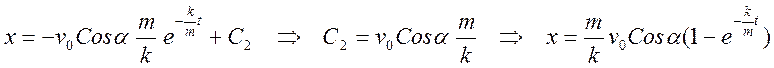           (3.3.2)

            Для оси y имеем уравнение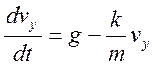

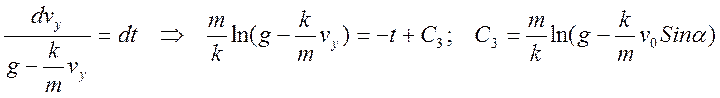
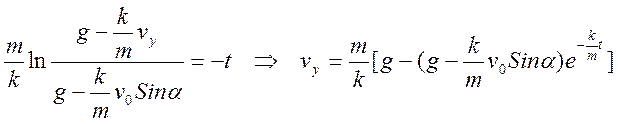
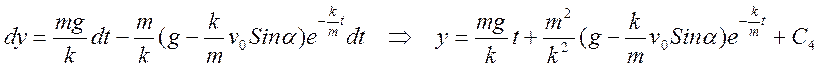
Определяя из начальных условий константу С₄ получим для координаты y закон изменения:

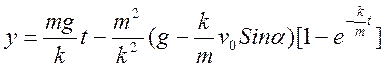   (3.3.3)

Исключив из уравнений (3.3.2) и (3.3.3) время, мы можем в принципе получить уравнение траектории, то есть y=f(x) для движения точки в плоскости (задача для тела, брошенного под углом к горизонту) при наличии силы сопротивления, пропорциональной скорости.