Неоднородные уравнения. Решение неоднородного уравнения

Неоднород. Ур-я.

y⁽ⁿ⁾+a₁y^(n-1)+…+a_n-1y`+a_n=f(t)

если f(t)=e^ptP(t), где P – степень полинома, исслед Эйлер

если P – не корень ур-я, то y=e^ptB(t), где В(t) – некий полином

Решение неоднородного ур-я = решение однородного+частное решение

Если Р – корень кратности α, y=t^αe^ptBИ(е)

Линейные системы уравнений.

1) dỹ/dt=A(t)ỹ(t)+f(t) (А – матрица) – с перемен. коэфф.

ỹ=(y₁,y₂…y_n); A=(a_ij(t)) – квадр матрица

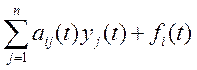В координатах dy_i/dt=

i=1,2…n

если f≡0 →однородная система, если нет →неоднородная

можно свести к 1 ур-ю (диф-м n раз) и каждый раз исключаем одно ур-е, затем решаем и подставляем в 1ое

Можно найти иначе: введем понятие ФСР однор ур-я →

ỹ₁(t),ỹ₂(t)…ỹ_n(t) – лин незав, каждая из них явл решением исх ур-я. это ФСР

(так же ввод опред Вронского, только из строк ỹ_i а не произв)

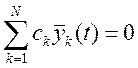 →с_k=0 → B(t)≠0

все тоже самое как и для однород ур-я

рассмотрим случай, когда матрица А не завис от t: dỹ/dt=Aỹ(t) – построим для него ФСР с пост коэфф 1ого порядка

будем искать решение в виде ỹ(t)=he^kt; k и h  не знаем

 → hk=Ah

проблема заключается в воиске собств вект матр А и собств числа,

надо найти h→сост лин сист отн h:

­_­

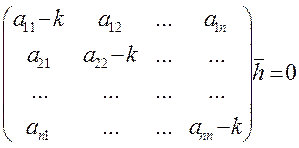
те (A-kE)h=0

det|A-kE|=0 – характ ур-е находим k, подст в ур-е и находим h

корни матр (если их n)→ они собств знач

A n лин зав h – собств векторы

имеет место результат

k₁-корень, α₁-кратность, h₁₁, h₁₂…h_1α1 – α₁ лин независ векторов →

домнож e^k1th₁₁, te^k1th₁₂… t^α1-1e^k1th_1α1            итд

               e^kmh­_m1, te­^kmth_m2…t^αm-1e^kmth_1mαm

эта сист ф-ий и будет фср

есть другой подход: рассмотрим такую задачу коши

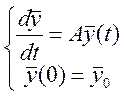
нам надо постр решение для t> или <0

если

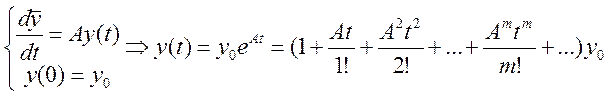
если туда подставить вместо числа А матр А получим:

ỹ(t)=e^tAỹ₀;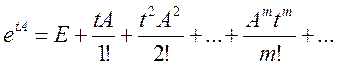

такой ряд сходится, он определяет матрицу.

тогда эта вектор-ф-я – решение задачи коши. проверка такая-же

Рассмотрим ур-е Шредингера

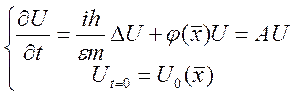
где Δ- опер Лапласа, А – оператор

нахождение решения – проблема квантовой механики

U(x,t)=e^tAU₀(x) – эта ф-ла дает формальное решение задачи коши

Если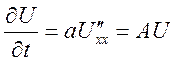

 

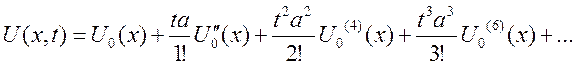
Оператор можно брать любой (только линейный)

t=0 →един матрица→ Эл-т

далее диф-ем док-во того что делается так, как будто А – число

можно 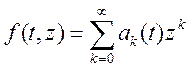- ряд, вместо z ставим матрицу 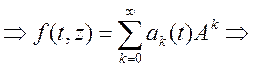мы сопоставили каждой аналит ф-ии операторную.