Чаще используются многослойные диэлектрические четвертьволновые покрытия из двух разнородных материалов, прозрачных для генерируемого излучения. Число слоев с чередующимся высоким nв и низким nн показателями преломления. Такая комбинация слоев равной оптической толщины обеспечивает синфазное отражение электромагнитной волны от всех границ раздела сред. В результате суммарная отраженная волна увеличивается по амплитуде, что эквивалентно повышению коэффициента отражения. Принцип работы такого интерференционного покрытия основан на том, что отражение от границы раздела при подходе излучения из менее плотной среды происходит с изменением фазы на π, а из более плотной - без скачка фазы. Следовательно, граница воздух (n0 = 1) - верхний слой (n = nв), приведет к изменению фазы первой отраженной волны на π. Отражение от границы между первым (nв) и вторым (nн) слоем произойдет без изменения фазы, но разность хода первой и второй волн, определяемая двойной толщиной слоя - λ/2, приведет к набегу фазы, равному π. Граница второго nн и третьего nв слоев даст суммарный набег фазы 3π и т.д. Таким образом, волны, отраженные от всех границ раздела сред, имеют одинаковые фазы колебаний. Коэффициент отражения интерференционного покрытия с ростом числа слоев стремится к единице (рис.3.5, а) и достигает у лучших образцов 99,8% [14]. При этом неотраженная часть излучения в отличие от металлических зеркал, не поглощается, а выводится из резонатора. Помимо основного максимума спектральная функция отражения имеет и менее интенсивные боковые (рис.3.5, б). Максимальный коэффициент отражения rmax многослойного покрытия из М слоев реализуется при строгом равенстве оптических толщин слоев четверти длины волны рабочего излучения: nвdв = nнdн = λ /4, где dв, dн - геометрические толщины слоев с высоким и низким показателями преломления. Величины dв и dн должны быть рассчитаны.
Рис.3.5. Зависимость коэффициента отражения интерференционного покрытия
от числа слоев (а) и длины волны (б): l = 0,63 мкм; n0 = 1 (воздух);
ns = 1,45 (стекло); 1 - nн = 1,35; nв = 2,3; 2 - nн = 1,45; nв = 1,95
Известны выражения для максимальных коэффициентов отражения многослойных покрытий [15]. Для нечетного числа слоев
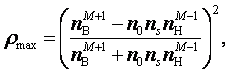(3.11)
для четного числа слоев
(3.12)
где n0 - показатель преломления окружающей среды (для воздуха n0 = 1); ns - показатель преломления материала подложки.
Выражения (3.11), (3.12) получены без учета паразитных потерь на зеркалах (a = 0). Поэтому пропускание, которое обеспечивает зеркало при данных условиях, находится как τ = 1 - ρmax. Путем расчетов с использованием (3.11), (3.12) определяется число слоев М, которое обеспечивает пропускание интерференционного покрытия τ = τопт. При выборе М следует стремиться к минимально возможному числу слоев, поскольку каждый из них вследствие поглощения и рассеяния излучения, отличия оптической толщины от λ/4 вносит дополнительные потери. Подбор материалов для λ/4-cлоев и подложек зеркал производится с учетом их оптических (табл.3.4 и 3.5), механических и термических свойств. Рекомендации по выбору материалов интерференционных покрытий и подложек зеркал, используемых в оптических резонаторах различных типов лазеров, изложены в разд.2.3 [1]. При прочих равных условиях большие значения ρmax и спектральной зоны максимального отражения обеспечиваются в случае использования материалов с сильно различающимися показателями преломления nB и nH.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.