Практические занятия и курсовое проектирование по дисциплине "Квантовые и оптоэлектронные приборы и устройства", страница 12

Iкр і ρудv0Li,

где ν0 - скорость квазистационарного движения границы расплава. Значение ν0 зависит от Is и от рода материала [3].

          Вторая проблема заключается в задании модели теплового источника для данного конкретного случая. В частности, она может быть представлена в виде одномерного поверхностного источника, для которого   В этом случае распределение температуры в пространстве и ее изменение во времени определяются теплопроводностью и описываются выражениями:

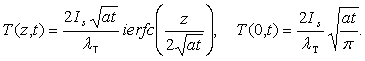
Для материалов, частично прозрачных для лазерного излучения, справедливо обратное соотношение . Здесь роль теплопроводности невелика и температура определяется проникновением излучения в материал:

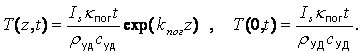
          Температурное поле движущегося источника тепла зависит от соотношения времени теплонасыщения материала (tнас ~ rmin2/a) и времени прохождения лазерным пучком rmin (rmin/v). Если время теплонасыщения меньше времени прохода пучка (vrmin < a), то источник можно считать медленным, при этом [11]

При обратном соотношении (vrmin > a) источник считается быстрым, максимум температуры сдвигается к периферии движущегося пучка противоположно направлению движения; величина Tmax  будет [11]

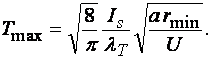
                Третьей   проблемой   является   зависимость   всех   коэффициентов

(aт, a, ρуд, суд) от температуры. В некоторых случаях возможно аналитическое решение (2.4) для той или иной модели. Вид получаемых функций T(x, y, z, t) иногда бывает достаточно сложен. Для исследования (2.4) наиболее целесообразны численные автоматизированные методы решения задачи. Они дают вид функций T = f(x, y, z, t) для различных условий.

          На кафедре имеется ряд программ для различных моделей источников и нагреваемых объектов. Работа с программами несложна, она протекает в диалоговом режиме и позволяет достаточно быстро произвести исследование технологического процесса и подобрать Pmin и rmin, обеспечивающие решение поставленной в задании задачи. Рассмотрим два примера.

          Первая задача - сварка встык металлических листов точечным источником, движущимся с постоянной скоростью. Заданы скорость процесса, толщина листа (h). Теплофизические параметры ряда металлов введены в программу.  Температура для модели квазистационарного нагрева в движущейся системе координат, связанной с источником нагрева, находится по формуле

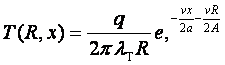
где R - пространственный радиус от начала координат до рассматриваемой точки. Решения для двух частных случаев приведены на рис.2.4.

          Варьируя  Pmin и ν, надо добиться, чтобы для изотермы T = Tпл, Dy (см. рис.2.4) было минимальным.

          Вторая задача. Пользуясь выражением  для температуры при импульсном нагреве тонкой пластины:

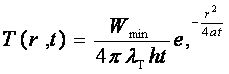
где r - расстояние от центра пятна, определить численно с помощью ЭВМ распределение температуры T = f(r) для разных моментов времени. На основании этих данных найти Wmin и t, достаточные для вскрытия в пластине отверстия заданного радиуса r1. Диапазоны допустимых изменений r - rmin и rmax и времени - tmin и tmax студент получает индивидуально у преподавателя. Теплофизические константы материалов введены в программу.