При определении температуры Te ионных лазеров на Ar и Kr близкий к практике результат получается с учетом эффекта вытеснения газа из разрядного капилляра при больших плотностях тока, используемых в этих лазерах. В результате эквивалентное давление газа, которое используется при подсчете произведения СрR, уменьшается в 1,5...2 раза. Для случаев многокомпонентных газовых смесей, которые используются, например, в гелий-неоновых и CO2-лазерах, использование универсальной кривой допустимо только для оценки величины Te. При этом для He-Ne лазера используется суммарное давление газовой смеси и параметры С и Ui для неона. При оценке Te плазмы CO2-лазеров учитываются параметры С и Ui для азота, а давление рассчитывается как сумма парциальных давлений углекислого газа и азота. Типичные соотношения парциальных давлений компонент газовых смесей для гелий-неонового лазера: He : Ne = (5...15) : 1, для CO2-лазера: CO2 : N2 : Не = 1 : (1...2) : (5...10). Электронная температура в плазме лазеров на парах металлов может быть оценена как для случая разряда в буферном газе - гелии.
Для точного определения температуры электронов в двух- и трехкомпонентных газовых смесях, используемых в ГРЛ, необходимым является решение трансцендентного относительно электронной температуры уравнения, получаемого из условия баланса заряженных частиц в цилиндрических разрядных промежутках. Решение этого уравнения связано с большим объемом вычислений, например методом последовательных приближений. Эти обстоятельства явились побудительным мотивом для разработки программы машинного расчета параметров плазмы газоразрядных лазеров, которая оказалась пригодной и для ионных лазеров.
Электронная температура для цилиндрического плазменного столба может быть определена из условия баланса зарядов в предположении превалирующего значения процесса прямой ионизации газа, что является допустимым для лазеров тлеющего разряда. Это условие связывает среднюю частоту ионизации ni с коэффициентом амбиполярной диффузии Da
![]() (3.1)
(3.1)
где R - внутренний радиус разрядного капилляра.
Коэффициент амбиполярной диффузии зависит от подвижности ионов bi и электронной температуры Te [8]
![]() (3.2)
(3.2)
где k - постоянная Больцмана; е - заряд электрона.
Из (3.1) и (3.2) имеем
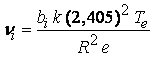 (3.3)
(3.3)
При аппроксимации сечения ионизации для молекул и газов линейной зависимостью qi(Te) = ai(kTe/e - Ui) [9], где ai - константа ионизации; Ui - потенциал ионизации, частота ионизации определяется как
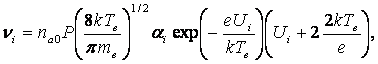
где na0 = 1/kTг - концентрация атомов газа при давлении р = 1 Па и температуре газа Tг; me - масса электрона.
Трансцендентное уравнение (3.1) применимо для однокомпонентных активных сред газоразрядных лазеров. Для многокомпонентных газовых смесей в левой части уравнения (3.3) следует использовать сумму частот ионизации всех входящих в смесь газов
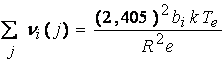 (3.4)
(3.4)
В этих условиях средняя подвижность газов может быть рассчитана с использованием закона Бланка [10]
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.