








Лекция № 14
Методы интегрирования уравнения переноса излучения и нахождения потока лучистой энергии.
Вклад радиационного поля в уравнение энергетического баланса сводится к определению дивергенции полного потока излучения, что связано с необходимостью решения уравнения переноса (13.13), проинтегрированного по углам и частоте. Решение этой задачи обычно также разбивается на два этапа: интегрирование по углам и интегрирование по частоте, однако, даже при таком подходе здесь приходится преодолевать серьезные математические трудности. Поэтому первоначально развились методы решения, использующие те или иные допущения. В первую очередь это предельные приближения, вообще не требующие решения уравнения переноса, когда поле излучения теряет интегральный по пространству характер и определяется лишь локальными параметрами среды. Они позволяют оперативно, на уровне оценок, определить перенос энергии излучением и получили широкое распространение в задачах, где не требуется точного и детального учета излучения. Другим примером упрощенного подхода является модель плоского слоя среды, часто применяемая в астрофизике при изучении переноса энергии в фотосферах звезд и в теории гиперзвукового обтекания тел.
Излучение плоского слоя
 В начале рассмотрим простейшую физическую модель – излучение
плоского слоя. В ряде случаев излучаемый объем газа может быть удовлетворительно
описан одномерной моделью плоского слоя, когда параметры состояния меняются поперек
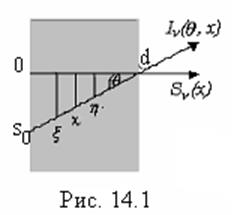
слоя. Совместим ось х с направлением нормали к поверхности слоя (рис.
13.1) Для выходящего из слоя потока излучения имеем
В начале рассмотрим простейшую физическую модель – излучение
плоского слоя. В ряде случаев излучаемый объем газа может быть удовлетворительно
описан одномерной моделью плоского слоя, когда параметры состояния меняются поперек
слоя. Совместим ось х с направлением нормали к поверхности слоя (рис.
13.1) Для выходящего из слоя потока излучения имеем
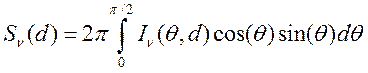 (14.1).
(14.1).
Подставляя в (14.1) выражение для интенсивности вдоль луча (13.12) в случае
отсутствия приходящего из вне излучения и переходя к оптической толщине 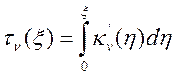
![]()
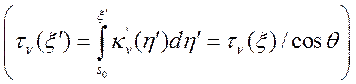 получим
получим
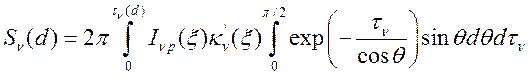 (14.2),
(14.2),
или
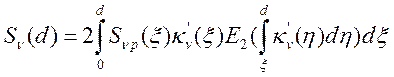 (14.3),
(14.3),
где ![]() - интегральная экспонента
- интегральная экспонента 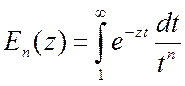 .
.
Поток излучения с поверхности плоского слоя называют еще яркостью поверхности.
С помощью формулы (14.3) легко написать выражение для потока ![]() в любой точке
в любой точке ![]() плоского
слоя толщиной d:
плоского
слоя толщиной d:
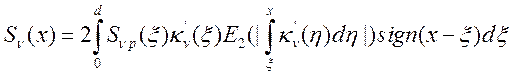 (14.4).
(14.4).
Если на границах 0 или d есть входящие из
вне потоки излучения нетрудно дописать дополнительные члены в (14.4) от этих
потоков, аналогично тому, как это было сделано в выражении (13.12) для ![]() . Эти члены выразятся через функции
. Эти члены выразятся через функции ![]() . Чтобы найти дивергенцию потока излучения,
входящую в балансовое уравнение энергии, нужно продифференцировать выражение (14.4)
и в результате получим
. Чтобы найти дивергенцию потока излучения,
входящую в балансовое уравнение энергии, нужно продифференцировать выражение (14.4)
и в результате получим
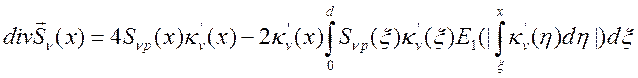 (14.5).
(14.5).
Рассмотрим в качестве частного случая плоский слой с постоянной температурой Т.
Яркость такого слоя согласно (14.3) есть:
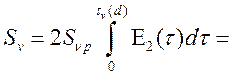
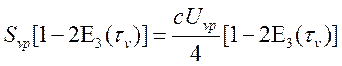 (14.6).
(14.6).
Она всегда меньше яркости абсолютно черного тела той же температуры и стремится к последней при tn ® ¥ (Е3 (¥) = 0). Очевидно, полупространство всегда излучает как черное тело.
Для оптически тонкого слоя tv << 1 имеем ![]() и
и
![]() (14.7).
(14.7).
Спектральную яркость поверхности неравномерно нагретого тела удобно
характеризовать эффективной или яркостной температурой ![]() равной
температуре абсолютно черного тела, посылающего с поверхности на данной частоте
точно такой же поток излучения, что и реальное тело.
равной
температуре абсолютно черного тела, посылающего с поверхности на данной частоте
точно такой же поток излучения, что и реальное тело.
Рассмотрим определение ![]() на примере плоского
слоя. Приравняем поток, определяемый выражением (14.3), к
на примере плоского
слоя. Приравняем поток, определяемый выражением (14.3), к ![]() :
: 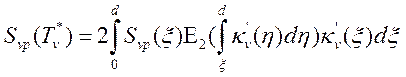 ,
откуда с учетом выражения для
,
откуда с учетом выражения для 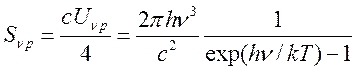 имеем уравнение для
определения
имеем уравнение для
определения ![]()
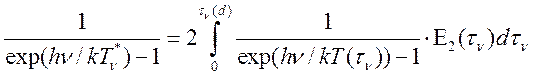 (14.8).
(14.8).
К такого рода приближениям относятся замена реальных излучающих объемов однородными, предположение об очень малой или большой оптической плотности объемов газа или комбинация указанных приближений.
Однородные модели.
Замена реального излучающего объема с переменными температурой и давлением объемом с постоянными (однородными) свойствами возможна лишь в некоторых задачах. Погрешность такого рода расчетов трудно контролировать. В то же время значительное упрощение вычислений и наличие в литературе данных по излучению однородных объемов обуславливает привлекательность такой методики.
Однородные модели используются в тех случаях, когда требуется оценить выходящий из объема поток излучения, а сам объем не сильно отличается от однородного. Наиболее просто спектральный поток лучистой энергии, падающий на единичную площадку, выделенную на границе излучающего объема определяется для плоского слоя и полусферического объема.
Для плоского слоя конечной толщины d и постоянной температуры поток излучения равен
![]() ,
, ![]() (14.9)
(14.9)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.