Методы интегрирования уравнения переноса излучения и нахождения потока лучистой энергии, страница 2

В случае полусферического объема радиуса R и постоянной температуры поток излучения через сферическую площадку в центре основания сферы равен

,                                                                         (14.10).

Приближение Планка.

В некоторых задачах весь спектр или значительная его часть может быть прозрачна для излучения, т.е. длина среднего свободного пробега фотонов намного больше характерного размера области . В этом случае оптическая толщина мала  и из уравнения для интенсивности 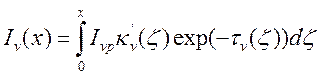 имеем , откуда следует, что  и .

Проинтегрируем уравнение переноса излучения (13.13) по углам 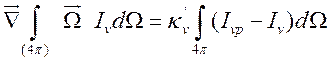 и  с учетом, что  и 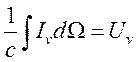 получим

                                                                                           (14.11) откуда в случае прозрачного излучения будем иметь

                                                                                          (14.12).

Проинтегрировав (14.12) по всему спектру, получим 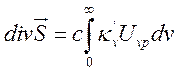. Если ввести среднее значение коэффициента поглощения и вынести его из под знака интеграла, то будем иметь:

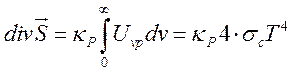                                                                     (14.13),

где

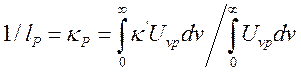                                                                    (14.14)

есть средний коэффициент Планка.

Приближение (14.13), (14.14) есть приближение объемного высвечивания, или приближение Планка.

Диффузионное приближение

Как мы уже видели, потери энергии вещества на излучение  в явной форме не зависят от углового распределения излучения и определяются только интегральными по направлению величинами. Если бы удалось вместо уравнения переноса интенсивности излучения  составить какие-то другие уравнения, для интегральных по направлению величин, то вопрос об угловом распределении излучения в уравнении энергии вообще бы не возникал. Одно такое уравнение (14.11) мы уже имеем. Оно содержит две неизвестные величины S_v и U_v и необходимо еще одно уравнение, которое можно получить только приближенно, наложив то или иное ограничение. Умножим уравнение (13.13) на  и вновь проинтегрируем по углам

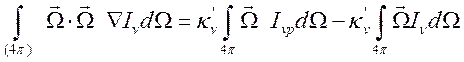                                             (14.15).

В (14.15) первый член в правой части равен нулю, а второй есть  и окончательно имеем:

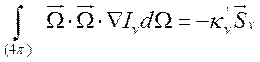                                                                          (14.16).

Теперь предположим, что поле излучения слабо анизотропно по направлениям и в первом приближении будем считать, что I_v в левой части уравнения (14.16) не зависит от W тогда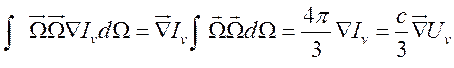 и получаем приближенную связь потока с плотностью излучения

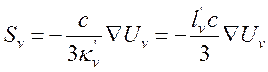                                                                         (14.17),

где  длина пробега для поглощения излучения. Если разделить (14.17) на hv получим связь потока квантов  с их плотностью N_v

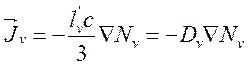                                                                            (14.18).

Уравнение (14.18) есть уравнение диффузии квантов с коэффициентом «диффузии» D_v аналогичное обычному уравнению диффузии частиц. Условием применимости диффузионного приближения, как известно, будет являться малость градиента плотности излучения, т.е. последняя должна мало меняться на расстоянии пробега излучения . Очевидно, что диффузионное приближение будет выполняться тем точнее, чем больше оптическая толщина тела. В случае оптически тонкого тела диффузионное приближение не справедливо. Как показывают расчеты, диффузионное приближение неплохо работает и в области .

Приближение Росселанда

Приближение Росселанда или как его еще называют лучистой теплопроводности справедливо для областей больших геометрических размеров или с большой плотностью частиц, когда значительная часть излучения заперта внутри области, т.е. длина пробега фотонов намного меньше характерного геометрического размера. В этом случае излучение близко к изотропному и для его описания мы воспользуемся диффузионным приближением (14.17), в котором в правой части заменим : 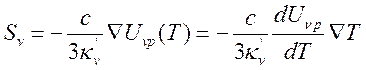. Интегрируя полученное уравнение по частоте и, вводя среднее значение длины свободного пробега излучения, получаем

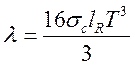,                                                                        (14.19),

где  имеет смысл коэффициента лучистой теплопроводности, а

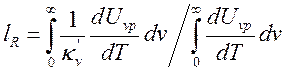                                                                      (14.20)

средний свободный пробег излучения (росселандово среднее).

Разбиение спектра по оптической плотности. Степени черноты.

Структура реальных спектров (рис.14.2) содержит значительное количество групп спектральных линий, вследствие чего оптическая плотность в таком спектре меняется в зависимости от частоты  до . Указанное обстоятельство наталкивает на мысль о том, что в ряде случаев можно разбить спектр на участки, в значительной части которых справедливо одно из указанных приближений. Роль же участков спектра с промежуточной плотностью оказывается малой. Анализ показывает, что такие случаи реализуются при давлениях ~ 1 бар и при температурах до  К.