 Вклад отдельных участков спектра в общем балансе
лучистых потерь может быть охарактеризован с помощью т.н. степени черноты,
определяемой как
Вклад отдельных участков спектра в общем балансе
лучистых потерь может быть охарактеризован с помощью т.н. степени черноты,
определяемой как
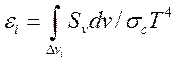 . (14.21).
. (14.21).
Полное значение e есть сумма ei по всем спектральным участкам, на которые разбивается полный спектр излучения
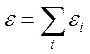 . (14.22).
. (14.22).
Как правило, для расчета степени черноты используются однородные модели плоского слоя и полусферического объема. Тогда согласно (14.9) и (14.10) можно записать для степени черноты плоского слоя и полусферического объема
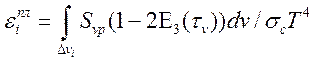 , (14.23),
, (14.23),
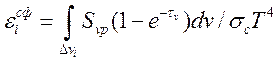 (14.24),
(14.24),
где ![]() ,
, ![]() –
толщина плоского слоя или радиус полусферического объема соответственно.
Разбиение спектра излучения на отдельные спектральные интервалы осуществляется
исходя из особенностей частотной зависимости коэффициента поглощения
–
толщина плоского слоя или радиус полусферического объема соответственно.
Разбиение спектра излучения на отдельные спектральные интервалы осуществляется
исходя из особенностей частотной зависимости коэффициента поглощения ![]() для каждого индивидуального вещества.
для каждого индивидуального вещества.
Данный подход в определении радиационных потерь может быть продуктивен в задачах радиационной газодинамики, если излучение носит объемный характер и геометрические особенности излучающего объема позволяют использовать приближение плоского слоя либо полусферического объема.
В этом случае при численном моделировании подобных задач учет лучистых
потерь может быть осуществлен следующим образом. Для каждой счетной ячейки (в
пределах которой температуру можно считать постоянной) вычисляется поток
лучистой энергии, от полусферического объема опирающегося на эту ячейку.
Используя известные степени черноты из (14.24) находим поток ![]() , который после приведения к излучению
единицы объема дает искомую мощность лучистых потерь
, который после приведения к излучению
единицы объема дает искомую мощность лучистых потерь 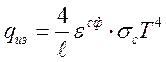 .
При этом из суммарной величины
.
При этом из суммарной величины 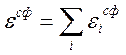 нужно исключить
степени черноты, соответствующие непрозрачным участкам спектра. Такой подход
позволяет правильно учесть радиационные потери, однако содержит не
контролируемую ошибку в определении температурного профиля, особенно при
наличии реабсорбции излучения. Тем не менее, расчеты высокотемпературных газодинамических
течений, выполненные в рамках данного подхода, дали хорошее качественное и
количественное совпадение с соответствующими экспериментальными результатами.
нужно исключить
степени черноты, соответствующие непрозрачным участкам спектра. Такой подход
позволяет правильно учесть радиационные потери, однако содержит не
контролируемую ошибку в определении температурного профиля, особенно при
наличии реабсорбции излучения. Тем не менее, расчеты высокотемпературных газодинамических
течений, выполненные в рамках данного подхода, дали хорошее качественное и
количественное совпадение с соответствующими экспериментальными результатами.
Кратко коснемся методов интегрирования уравнения переноса излучения по частоте. Вначале заметим, что в предельных случаях и при использовании степени черноты, полученные результаты уже являются интегральными по углам и частоте. В остальных случаях, на практике, задача сводится к осреднению спектрального коэффициента по частоте тем или иным способом.
Приближение «серой материи».
Предположим, что коэффициент поглощения не зависит от частоты и является функцией только температуры и давления вещества:
![]() (14.25).
(14.25).
Среда, для которой выполняется равенство (14.25) получила название «серой материи».
Проинтегрируем исходное уравнение переноса по частоте с учетом (4.25):
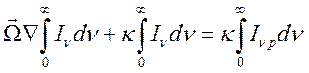 (14.26),
(14.26),
откуда с учетом
того, что 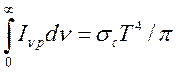 из (14.26) следует уравнение для интенсивности
излучения не зависящее от частоты
из (14.26) следует уравнение для интенсивности
излучения не зависящее от частоты
![]() (14.27).
(14.27).
Следует сказать, что приближение «серой материи», следует использовать с большой осторожностью, поскольку оно во многих случаях приводит к качественно и количественно неверным результатам.
Многогрупповое приближение.
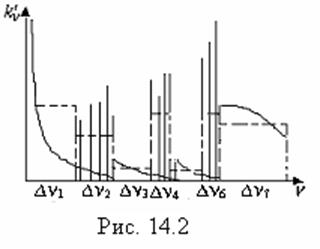
Это приближение основывается на предварительном анализе спектрального
коэффициента поглощения конкретного вещества, когда весь спектр ![]() разбивается на конечное число групп –
частотных интервалов (см. рис.14.2), в каждом из которых вводится некий
усредненный коэффициент поглощения
разбивается на конечное число групп –
частотных интервалов (см. рис.14.2), в каждом из которых вводится некий
усредненный коэффициент поглощения
![]() (14.28).
(14.28).
Для определения уравнения, которому удовлетворяет ![]() проинтегрируем
уравнение переноса по частоте от
проинтегрируем
уравнение переноса по частоте от ![]() до
до ![]() :
:
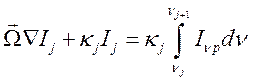 (14.29).
(14.29).
Правую часть уравнения (14.29) представим в виде
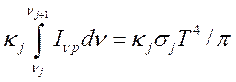 (14.30),
(14.30),
где 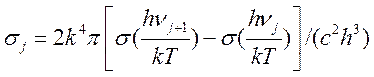 . Для вычисления функции
. Для вычисления функции 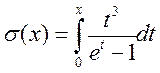 можно использовать приближенные формулы
можно использовать приближенные формулы
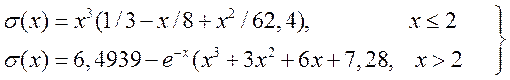 (14.31).
(14.31).
Очевидно, данное приближение будет тем точнее, чем больше число групп (частотных интервалов).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.