


|
Задание для контрольной работы по теоретической механике (кинематика К4) |
|
|
|
A) Плоский механизм состоит из стержней 1, 2, 3, 4 и ползуна B, соединенных друг с другом и с неподвижными опорами О1, О2 шарнирами. Точка D находится в середине стержня AB. Длины стержней равны соответственно l1=0.4 м, l2=1.2 м, l3=1.4 м. Положение механизма определяется углами a=60°, b=150°, g=90°, j=30°, q=30°. Звено 1 вращается с угловой скоростью w1=2 с-1и угловым ускорением e1=7 с-2. Найти скорости точек B и Е, угловую скорость звена DE, ускорение точки B и угловое ускорение звена AB. B) Плоский механизм состоит из стержней 1, 2, 3, 4 и ползуна B, соединенных друг с другом и с неподвижными опорами О1, О2 шарнирами. Точка D находится в середине стержня AB. Длины стержней равны соответственно l1=0.4 м, l2=1.2 м, l3=1.4 м. Положение механизма определяется углами a=60°, b=150°, g=90°, j=30°, q=30°. Ползун В движется со скоростью vВ=3 м/с и ускорением aВ=4 м/с2. Найти скорости точек A и Е, угловую скорость звена DE, ускорение точки A и угловое ускорение звена AB. |
Решение задачи A)
|
|
1. Строим положение механизма в соответствии с заданными углами. 2. Определяем vB. Сначала определяем скорость точки A, как точки кривошипа O1A, вращающегося с угловой скоростью w1: vA=w1l1=0.8м/с (скорость точки А перпендикулярна кривошипу O1A и составляет со звеном AB угол 60°). Скорость точки B направлена вдоль направляющих ползуна B и составляет с направлением звена AB угол 30°. Точки A и B принадлежат звену AB и для скоростей этих точек выполняется теорема о проекциях: vACos60°= vBCos30°. Отсюда vB=(Cos60°/Cos30°)vA=0.462м/с. 3. Определяем vЕ. Для этого сначала определим скорость точки D. Найдем мгновенный центр скоростей (МЦС) звена AB. Это будет точка Р (пересечение перпендикуляров к скоростям vA и vB). Звено AB совершает поворот вокруг МЦС (точки Р) с угловой скоростью |
wBA=vA/AP=vB/BP=0.667c-1. Точка D как точка звена AB имеет скорость vD=wBADP=0.462м/с (треугольник DBP равносторонний и DP=DB=(1/2)AB=(1/2)l3). Скорость точки D перпендикулярна радиусу вращения DP и составляет угол 60° со звеном DE. Точка E как точка кривошипа O2E вращается вокруг центра O2 и ее скорость перпендикулярна кривошипу O2E. Тем самым она составляет угол 60° со звеном DE. Для точек E и D как точек звена DE также выполняется теорема о проекциях, то есть vDCos60°= vECos60°, отсюда vD= vE=0.462м/с.
4. Определяем wDE. Для определения угловой скорости вращения звена DE найдем его мгновенный центр скоростей. Это будет точка P1 (пересечение перпендикуляров к скоростям точек vD и vE).
Находим wDE= vD/DP1= vE/EP1=0.667 c-1 (стороны DP1 и EP1 находим из равнобедренного треугольника P1DE, его основание DE=l2 ).
5. Определяем aB. и eBA. Для определения ускорения точки B и углового ускорения звена AB выберем за полюс точку A и воспользуемся формулой, связывающей ускорения двух точек твердого тела (звена AB):
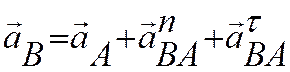 (*)
(*)
Ускорение точки A найдем, учитывая, что точка A принадлежит кривошипу O1A, вращающегося с угловой скоростью w1 и угловым ускорением e1: aAn=w12O1A=1.6м/c2, aAt =e1 O1A=2.8м/c2 (ускорение aAn направлено от точки A к центру вращения O1, ускорение aAt направлено перпендикулярно кривошипу O1A).
Центростремительное ускорение точки B из-за вращения вокруг полюса A aBAn=wAB2AB и направлено от точки B к полюсу A (угловая скорость звена AB wBA была найдена при определении скорости точки D).
Тангенциальное ускорение точки B из-за неравномерного вращения вокруг полюса A aBAt = eBAAB и направлено перпендикулярно звену AB (предполагаем, что направление дуговой стрелки углового ускорения eBA такое же как и угловой скорости wBA, если же это не так, то при последующих вычислениях мы получим отрицательное значение углового ускорения eBA).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.