Ускорение точки B направлено вдоль направляющих ползуна B.
Проведем оси Axy (ось x совпадает с направлением звена AB, ось y перпендикулярна звену AB). Спроектируем равенство (*) на оси Axy учитывая, что ускорение точки A может быть представлено как векторная сумма ускорений aAn и aAt :
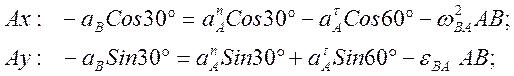
Из этой системы уравнений найдем искомые aB=0.733 м/с2 и eBA=2.57 c-2.
Ответ : vB=0.462м/с, vE=0.462м/с, wDE= 0.667 c-1, aB=0.733 м/с2, eBA=2.57 c-2.
Решение задачи B)
|
|
1. Строим положение механизма в соответствии с заданными углами. 2. Определяем vA. Скорость точки B направлена вдоль направляющих ползуна B и составляет с направлением звена AB угол 30°. Скорость точки A (как точки кривошипа O1A) перпендикулярна кривошипу O1A и составляет со звеном AB угол 60°. Точки A и B принадлежат звену AB и для скоростей этих точек выполняется теорема о проекциях: vACos60° = vBCos30°. Отсюда vA=(Cos30°/Cos60°)vB=5.2м/с, что позволяет также определить w1=vA/l1=12.98с-1 3. Определяем vЕ. Для этого сначала определим скорость точки D. Найдем мгновенный центр скоростей (МЦС) звена AB. Это будет точка Р (пересечение перпендикуляров к скоростям vA и vB). Звено AB совершает поворот вокруг МЦС (точки Р) с угловой скоростью |
wAB=vA/AP=vB/BP=4.29c-1. Точка D как точка звена AB имеет скорость vD=wBADP=3.0м/с (треугольник DBP равносторонний и DP=DB=(1/2)AB=(1/2)l3). Скорость точки D перпендикулярна радиусу вращения DP и составляет угол 60° со звеном DE. Точка E как точка кривошипа O2E вращается вокруг центра O2 и ее скорость перпендикулярна кривошипу O2E. Тем самым она составляет угол 60° со звеном DE. Для точек E и D как точек звена DE также выполняется теорема о проекциях, то есть vDCos60°= vECos60°, отсюда vD= vE=3.0м/с.
4. Определяем wDE. Для определения угловой скорости вращения звена DE найдем его мгновенный центр скоростей. Это будет точка P1 (пересечение перпендикуляров к скоростям точек vD и vE).
Находим wDE= vD/DP1= vE/EP1=4.33 c-1 (стороны DP1 и EP1 находим из равнобедренного треугольника P1DE, его основание DE=l2 ).
5. Определяем aA. и eAB. Для определения ускорения точки A и углового ускорения звена AB выберем за полюс точку B и воспользуемся формулой, связывающей ускорения двух точек твердого тела (звена AB):
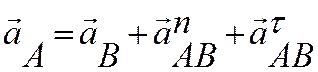 (*)
(*)
Ускорение точки A найдем, учитывая, что точка A принадлежит кривошипу O1A, вращающегося с угловой скоростью w1, и ее нормальное ускорение, направленное к точке О1, равно aAn=w12O1A=67.4 м/c2. Ускорение aAt нам не известно, но оно направлено перпендикулярно кривошипу O1A, то есть составляет угол 60° с направлением звена AB. В силу этого формулу (*) перепишем в виде:
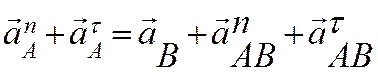 (**)
(**)
Центростремительное ускорение точки A из-за вращения вокруг полюса B aABn=wAB2AB=22.08 м/c2 и направлено от точки A к полюсу B (угловая скорость звена AB wBA была найдена при определении скорости точки D).
Тангенциальное ускорение точки A из-за неравномерного вращения вокруг полюса B aABt = eABAB и направлено перпендикулярно звену AB (предполагаем, что направление дуговой стрелки углового ускорения eAB такое же как и угловой скорости wAB, если же это не так, то при последующих вычислениях мы получим отрицательное значение углового ускорения eAB).
Ускорение точки B направлено вдоль направляющих ползуна B.
Проведем оси Bxy (ось x совпадает с направлением звена AB, ось y перпендикулярна звену AB) и спроектируем равенство (**) на оси Bxy :
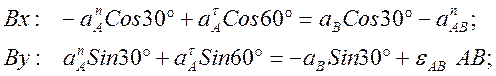
Из первого
уравнения найдем aAt =79.5 м/с2, что дает нам ![]() =104.2 м/с2
=104.2 м/с2
Из второго уравнения получим eAB =74.7 c-2.
Ответ : vA=5.2м/с, vE=3.0м/с, wDE= 4.33 c-1, aA=104.2 м/с2, eAB=74.7 c-2.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.