Классификация гелиетрических аберраций оптических систем

ЛЕКЦИЯ

КЛАССИФИКАЦИЯ ГЕЛИЕТРИЧЕСКИХ аберрациЙ оптических систем

Рассматриваем отклонение траекторий распространения пучка световых лучей от параксиальных. Введем две системы координат: в пространстве предметов (x₀, y₀, 0) и в пространстве изображений (x₁, y₁, 0). Будем рассматривать, во что превратится точка P₀ из пространства предметов. Если оптическая система не вносит искажений (например, в парксиальном приближени), то в пространстве изображений также будет точка P₁. Этой точке на выходном зрачке оптической системы можно поставить в соответствие сферический волновой фронт с центром кривизны в точке P₁, называемый опорной сферой Гаусса. Если взять какой-нибудь другой луч (не главный), исходящий из P₀ и отличающийся от параксиального, то он пересечет плоскость изображений не строго в точке P₁, а в другой точке P₁^*. Вектор

                                                       (1)

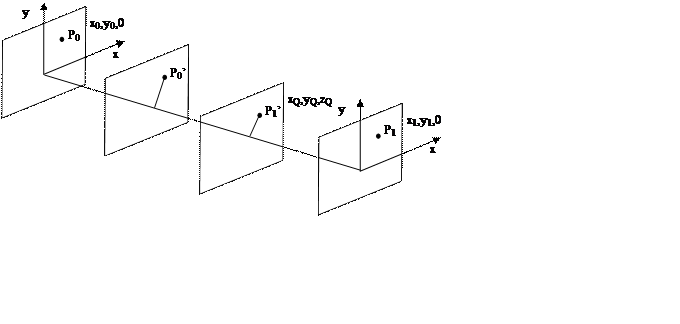
Называется лучевой аберрацией. Изображению P₁^* можно сопоставить волновой фронт W, проходящий через центр выходного зрачка и соответственно формирующийся с участием главного луча. Обозначим символом Q точку пересечения нашим непараксиальным лучом опорной сферы Гаусса, символом Q^* обозначим точку пересечения с волновым фронтом W. Оптический путь (эйконал) Ф=[QQ^*] называется волновой аберрацией.

Установим функциональную связь между лучевой и волновой аберрацией и некоторые функциональные свойства лучевой и волновой аберраций. Очевидно, что функция Ф=[QQ^*] зависит от положения точки P₀ и лучей формирующих изображение P₁^*. При этом мы заранее считаем, что в формировании P₁^* участвует главный луч, проходящий через центры входного и соответственно выходного зрачка. Тогда Ф=[QQ^*] можно представить в виде.

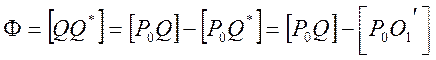                                                      (2)

Здесь расстояния [P₀Q^*] и [P₀O₁’] равны поскольку точки Q^* и O₁’ принадлежат одному и тому же волновому фронту, формирующему изображение P₁^*. Т.к. Ф=[QQ^*] – это расстояние между Q^* и O₁’, то она является функцией координат предмета и координат пересечения лучей с плоскостью выходного зрачка и  может быть записана как:

                              (3)

Здесь D₁ – z-координата центра выходного зрачка в пространстве изображений. Точка Q принадлежит опорной сфере Гаусса, поэтому между координатами x_Q, y_Q, z_Q существует функциональная связь:

                                                            (4)

Т.о. z_Q исключается из формулы (3) и функция волновой аберрации оказывается зависящей от четырех переменных:

                                                            (5)

Связь лучевой и волновой аберрации найдем из геометрических построений. В силу подобия треугольника образованных лучам, перпендикулярными к волновым фронтам и соединяющими точки Q иQ^* с точками P₁, и P₁^* и треугольника образованного точками Q иQ и пересечением волновых фронтов с осью z₁  сразу можно написать соотношение.

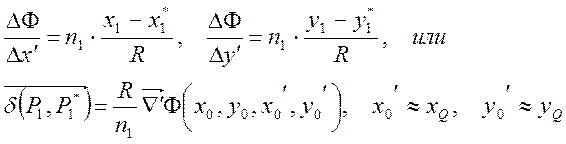                                      (6)

Здесь штрихованные координаты относятся к плоскости выходного зрачка, градиент берется по трихованным координатам, для перехода к эйконалу учтен показатель преломления n₁.

       Несколько другие рассуждения. Пусть точка P₁ с координатами x₁ и y₁ сформирована сферическим волновым фронтом,  проходящим через центр выходного зрачка (с участием главного луча). Уравнение этого сферического волнового фронта (опорной сферы Гаусса) –  это уравнение сферической поверхности:

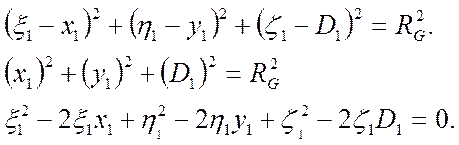                                                            (1*)

Греческие буквы – координаты сферы в зоне выходного зрачка. Если повернуть систему координат в пространстве изображений, так чтобы ось z совпала с главным лучом, то точка  P₁ окажется в начале координат. Уравнение опорной сферы Гаусса упростится:

                                                            (2*)

Для P₁^*, связанной с лучевой аберрацией уравнение волнового фронта, очевидно будет следующим:

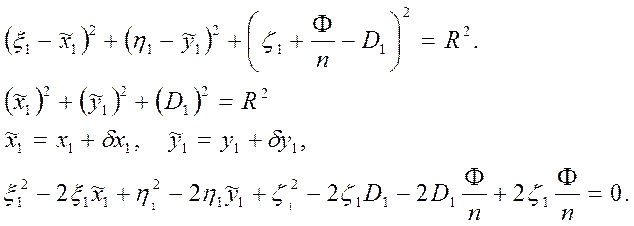                                                 (3*)

Разность между опорной сферой Гаусса и новым волновым фронтом – волновая аберрация.  Вычтем из (3*)  (2*):

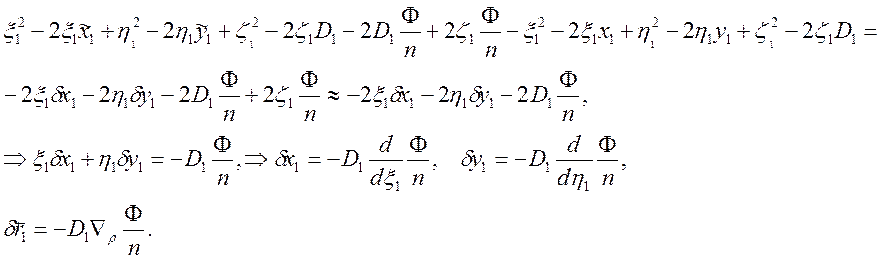(4*)

Тем самым  установлена связь между волновой и лучевой аберрацией. Поскольку Ф зависит от координат изображения и координат луча в плоскости выходного зрачка,  плоскость изображения сопряжена с плоскостью предметов, а плоскости входного и выходного зрачков также сопряженные, то Ф=Ф(x₀,y₀,ζ₀,η₀). Для центрированных систем с аксиальной симметрией зависимость  Ф(x₀,y₀,ζ₀,η₀) также должна обладать аксиальной симметрией. Следовательно Ф(x₀,y₀,ζ₀,η₀) можно представить в виде разложения по инвариантам вращения системы координат вокруг оси z. Инварианты вращения строятся из векторов r и ρ:

                     

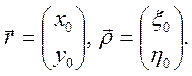
Имеется 3 инварианта вращения (rr), (ρρ), (rρ). Поскольку волновая аберрация является отклонением от опорной сферы Гаусса, то разложение  Ф(x₀,y₀,ζ₀,η₀) начинается лишь с 4-х степеней переменных (квадратам степеней – соответствует сферическая поверхность, порождающая стигматическое изображение):

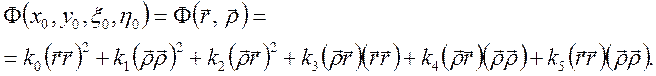                              (5*)

Дифференцируя разложение волновой аберрации по координатам луча на входном (выходном) зрачке получим разложение для лучевой аберрации:

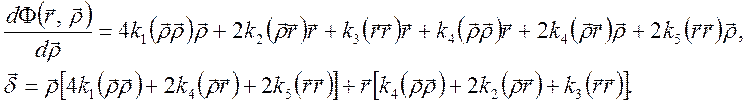                              (6*)

Классификацию геометрических аберраций удобно делать в безразмерных переменных, предложенных Зайделем. Для этого вводятся масштабы длины в пространстве предметов и изображений L₀ и L₁, а также  аналогичные линейные масштабы для сопряженных плоскостей входного и выходного зрачков - l₀ и l₁. Т.е. размер предмета и изображения следует выражать в единицах L₀ и L₁ соответственно. Очевидно, что отношение L₁/L₀  - это поперечное увеличение. Отклонение луча от оптической оси на входном и выходном зрачках (высота луча) выражается в единицах l₀ и l₁ соответственно. В этих единицах высоты лучей на  входном и выходном зрачках одинаковы. В качестве новых координат в пространстве предметов и изображений примем: