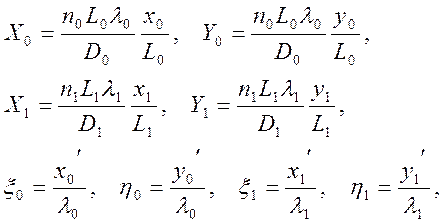Классификация гелиетрических аберраций оптических систем, страница 2

                                                            (7)

Здесь D₀ – расстояние от плоскости предметов до плоскости входного зрачка. Первый множитель в формулах (7) – это инвариант Лагранжа-Гельмгольца для масштаба в параксиальном приближении. Координаты луча в переменных Зайделя сохраняют свое численное значение на протяжении всей оптической системы. Формула (6) в переменных Зайделя принимает более простой вид:

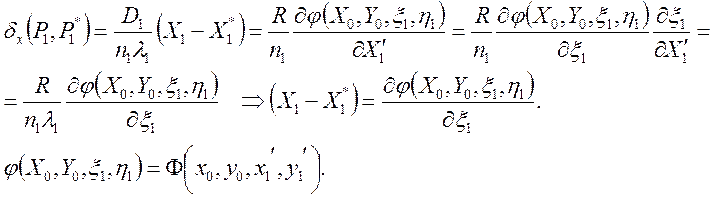(8)
Классификацию геометрических аберраций будем делать в переменных Зайделя, считая что оптическая система центрирована и обладает аксиальной симметрией. Считаем, что аберрации не очень велики, поэтому аберрации будем искать в виде разложения по переменным Зайделя в цилиндрической системе координат:

                                                           (9)

При аксиальной симметрии остаются лишь 3 независимые переменные r, r, (Q-Q₀), поэтому в окончательный ответ войдут лишь инварианты вращения. Их можно составить всего 3:

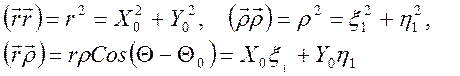                                                            (10)

Свойства аберраций проще понять, анализируя форму аберрационной кривой, которая является границей изображения точки, когда лучи полностью заполняют входной зрачок. Фактически аберрационная кривая порождается лучами проходящими вблизи периметра входного зрачка. Из-за аксиальной симметрии следует, что в функцию волновой аберрации могут входить лишь четные степени инвариантов вращения (10). Разложение начинается с четвертых степеней, поскольку квадратичным слагаемым отвечает сферический волновой фронт. Отклонение его от опорной сферы Гаусса дает лишь одну аберрацию, называемую дефокусировкой,  Она устраняется перемещением плоскости изображений вдоль оси z и при точной настройке (в параксиальном приблтжении) на резкое изображение квадратичные слагаемые исчезают. Минимальный порядок разложения для лучевой аберрации соответственно – кубический. В самом общем виде форма аберрационной кривой описывается уравнением:

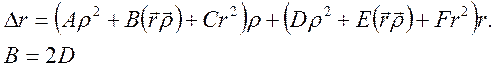                                                            (11)

A, B, C, D, E, F – постоянные коэффициенты зависящие от устройства оптической системы и положения предметной плоскости, r – в данном случае радиус выходного (из выходного в переменных Зайделя это не важно) зрачка. Удобно каждое из слагаемых в (11) рассмотреть по отдельности

Если предмет (точка) расположен на оси оптической системы, то r=0, и из всей суммы (11) останется одно слагаемое.

                                              (12)

Отклонение от параксиального фокуса следует за лучом проходящим по периметру входного зрачка и аберрационная кривая – окружность с центром лежащим на оптической оси и радиусом Ar³. Все остальные аберрации при этом исчезают

Учтем теперь слагаемые линейные по отклонению предмета от оптической оси:

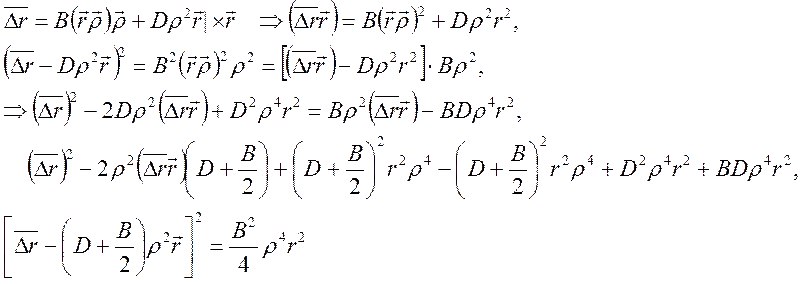                              (13)

Уравнение (13) описывает семейство окружностей радиусом Br²|r|/2 со смещенными в направлении положения предмета-точки центрами:

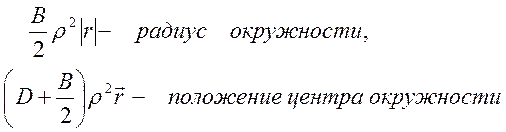                                                       (14)

По мере увеличения диаметра зрачка увеличивается радиус аберрационной окружности, и положение ее центра удаляется от оптической оси.

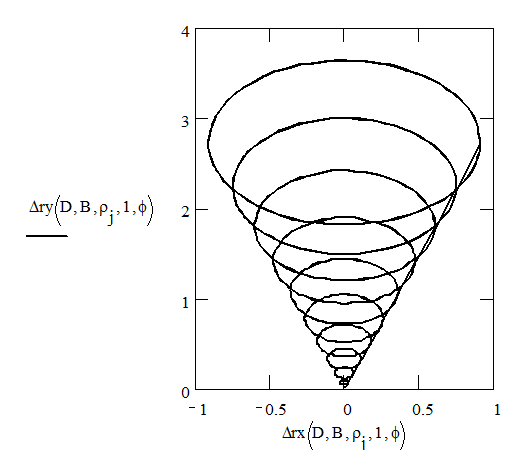Характерный вид изображен на рис. Огибающая граница напоминает комету хвостом Раствор угла огибающей 60^о (B=2D).

Следующий тип аберраций, пропорционален r² называется астигматизм косых пучков и искривление плоскости изображения. Если все коэффициенты в (11) кроме C и E равны нулю, уравнение аберрационной кривой принимает вид:

                                                                                      (15)

Для упрощения будем считать, что смещение точки-объекта происходит в направлении оси Y. Тогда декартовы компоненты аберрационной кривой будут следующими:

                                                                                         (16)

Уравнение (16) описывает эллипс с центром в параксиальном фокусе на расстоянии D₁ от выходного зрачка и полуосями равными СY₀²r и(С+Е)Y₀²r, параллельными выбранным нами ортам. На другом расстоянии от выходного зрачка в силу прямолинейного распространения света уравнения (16) легко привести к виду:

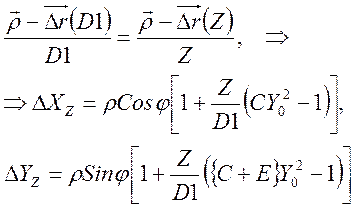                                                                                             (17)

Здесь в качестве оси Z взят вектор, идущий из центра выходного зрачка в параксиальный фокус. Из (17) видно, что эллипс может вырождаться в отрезки прямых, когда DX_Z или DY_Z обращаются в ноль. Эти отрезки называемые фокальными отрезками, они параллельны декартовым ортам. Разность продольных координат для фокальных отрезков называется астигматической разностью R_A.

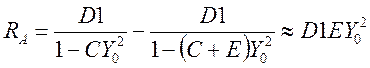                                                                                             (18)

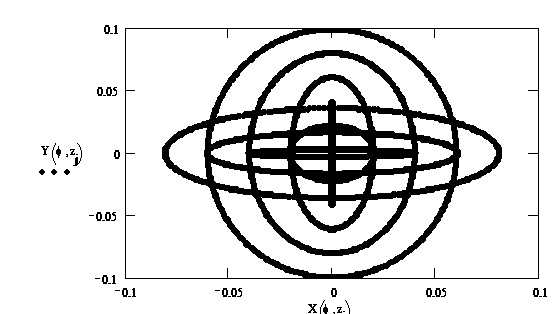
Форма аберрационных кривых приведена на рисунке, она дает представление о форме каустике лучей.

Если все коэффициенты в (11) кроме F равны нулю происходят искажения предмета независящие от диаметра входного (выходного) зрачка. При этом точка предмета дает точку в изображении. Однако координата изображения нелинейно зависит от координаты предмета:

                                                                                         (19)

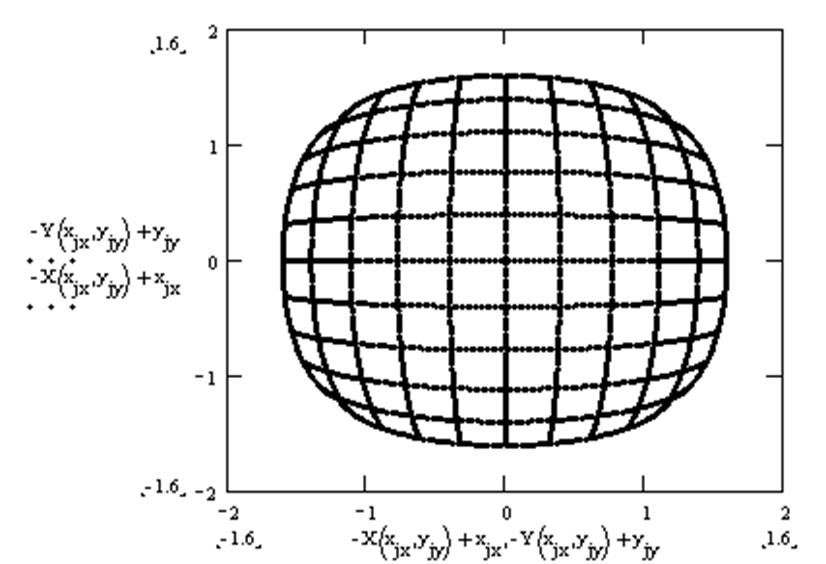
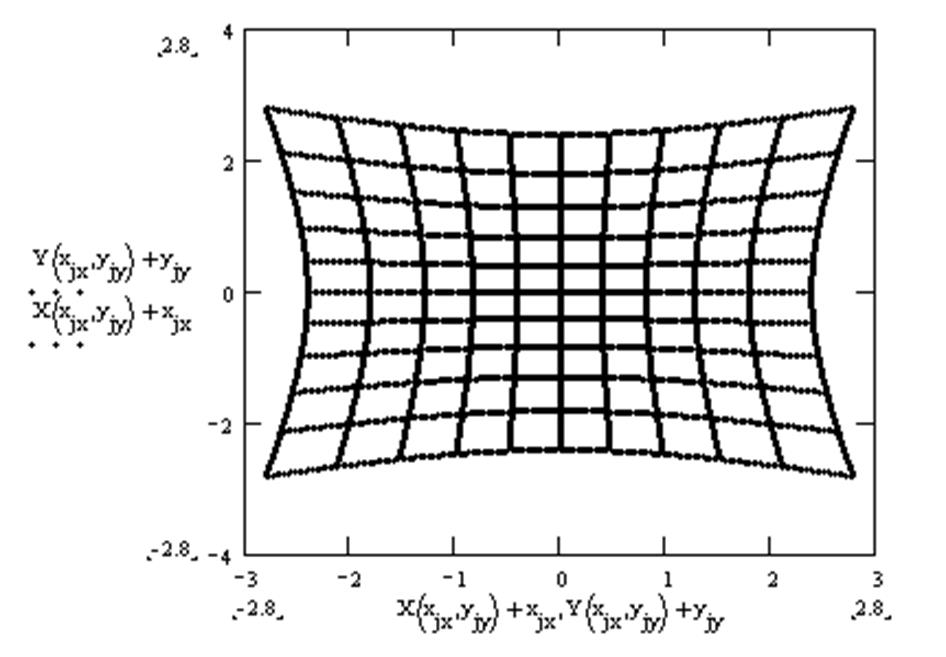
Наблюдаемое искажение изображения называется дисторсией. Прямые линии, проходящие через главную оптическую ось изображаются прямыми. Все прочие прямые линии искривляются.