Вогнутая дифракционная решетка

ЛЕКЦИЯ

 Вогнутая дифракционная решетка.

Вогнутые ДР – это сферическая поверхность со штрихами, обладающие как диспергирующими, так и фокусирующими свойствами. Применение вогнутых ДР позволяет обойтись без фокусирующей оптики в спектральном приборе – без коллиматорного и камерного объективов. Вогнутые ДР обычно применяются в диапазоне от 1000Å до 10 Å. В этом диапазоне нет прозрачных материалов, пригодных для изготовления линзовой оптики, а коэффициеты отражения металлов при малых углах падения (почти по  нормали) существенно уменьшаются. Поэтому у спектральных приборов с плоскими ДР существенно снижается светосила. Применение схем приборов со скользящим падением  лучей увеличивает светосилу, но сильно возрастают внеосевые аберрации. В случае вогнутой ДР используется одна отражающая поверхность со скользящим падением. И хотя внеосевые  аберрации также велики, приборы с вогнутой ДР оказываются более эффективными.

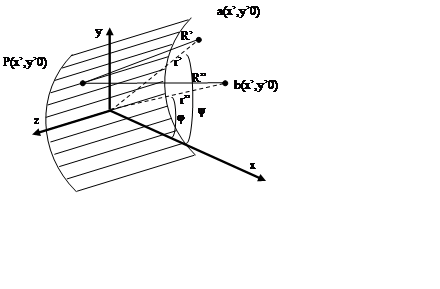
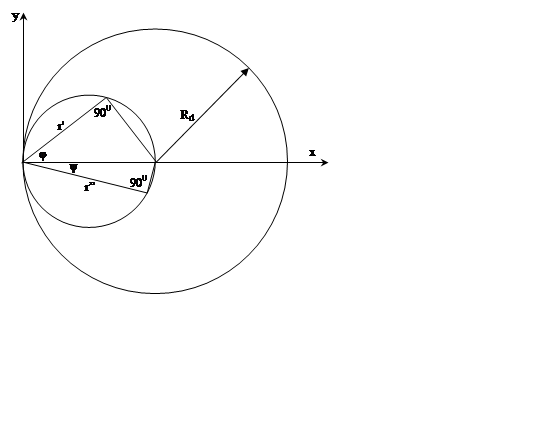
Теория вогнутой ДР. Возьмем участок сферической поверхности с радиусом R_d,  касательный к плоскости yz. Точка a(x’,y’,z’=0) – точечный источник, расположенный в плоскости xy. Регистрировать интенсивность излучения будем в точке b(x”,y”,z”=0), расположенной также в плоскости xy. Пусть на решетку нанесены штрихи, параллельные оси z. В случае вогнутой ДР заранее неизвестно вдоль какой линии должна воспроизводиться периодичность структуры, вдоль оси y или вдоль дуги окружности. Произвольная точка P(x,y,z) на ДР – это источник вторичных волн. Выразим длины оптических путей aP=R’ и bP=R” через их координаты при условии, что R, aP, bP много больше размера решетки:

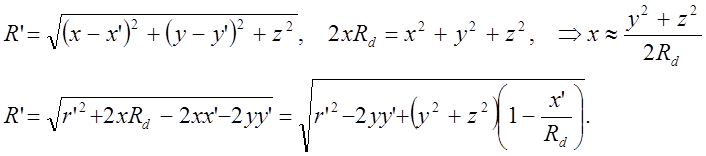          (1)

Здесь учтено, что вторичный источник расположен на сфере, радиус которой значительно превышает размер ДР (R_d>>y,z). Далее проведем разложение (1) по степеням координат вторичных источников на ДР до квадратов:

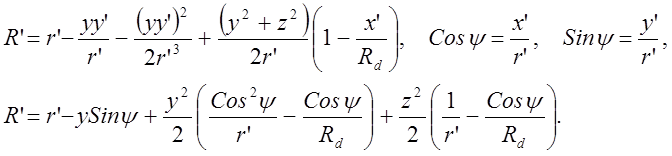                    (2)

Данное разложение отвечает уже задаче о дифракции Френеля. Аналогичное выражение можно получить дли пути от вторичного источника в точку наблюдения:

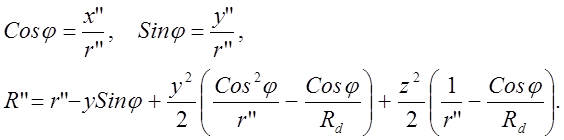                                      (3)

Суммарный оптический путь от источника до точки наблюдения – сумма R’+R”. Определим закон расположения штрихов на поверхности ДР из условия – изменение полного оптического пути (разность хода) при переходе от какого либо штриха к соседнему оставалась постоянной. Если эта разность хода равна целому числу длин волн, то вторичные волны будут приходить в точку наблюдения в одной фазе и это будет направление на интерференционный максимум:

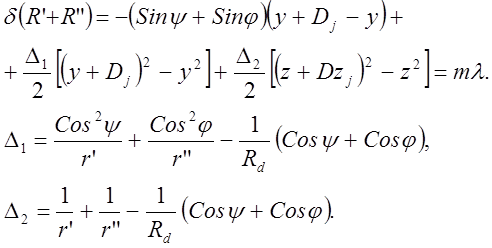                                                  (3)

Чтобы удовлетворить условию периодичности меридиональном сечении (z=0) необходимо положить Δ₁=0 (величины Δ₂ и Δ₁ при заданных углах падения и дифракции остаются постоянными). Тогда первое слагаемое в (3) удовлетворяет условию периодичности если все D_j=D  Но тогда и величина Δ₁ должна обратиться в ноль. Тогда условие образования интерференционного максимума будет похоже на аналогичное условие для плоской решетки:

. (4)                                                                                         (4)

При этом штрихи должны быть равномеро расположены вдоль координаты y, а не вдоль дуги окружности.  Смысл выражения (4) в том. что при заданном расположении точечного источника (при заданном угле ψ) угол φ определяет направление на интерференционный максимум для определенной длины волны λ в определенный порядок дифракции m. Таким образом происходит пространственное спектральное разложение. Условие обращения в ноль величин Δ₂ и Δ₁ фактически определяет значения расстояний от источника до решетки и от решетки до точки наблюдения.

Рассмотрим сначала участие точек дифракционной решетки в области z=0. Тогда важно лишь обращение в ноль Δ₁:

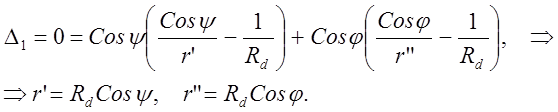                                   (5)

Равенства (5) показывают, что точки a(x’,y’,z’=0) и b(x’,y’,z’=0)  расположены на окружности, касательной к ДР и диаметром равным R_d. Это легко понять из рассмотрения вписанных в окружность с радиусом R_d/2 прямоугольных треугольников, гипотенуза которых – диаметр окружности. перпендикулярна к ДР в точке касания и с углами между катетом и гипотенузой – ψ и φ. Этот круг с радиусом R_d/2 называется кругом Роуланда. Углы, образованные пучком лучей падающих из точки a(x’,y’,z’=0) и лучами, дифрагированными в точку b(x’,y’,z’=0), можно рассматривать как вписанные в круг Роуланда. Поэтому в точке b(x’,y’,z’=0) появится  монохроматическое изображение  точечного источника – вогнутая решетка обладает фокусирующим действием.

В саггитальном сечении должно выполняться Δ₂=0. При этом r” получается несколько иным.

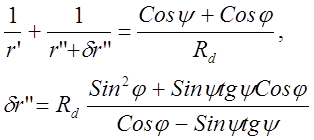                                                                           (6)

Величина δr” – определяет астигматизм вогнутой ДР.

Из подобия треугольников и величины астигматической разности можно найти величину (высоту) изображения источника:

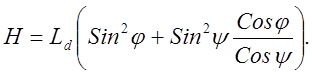                                                                                (6’)

Угловая дисперсия может быть найдена дифференцированием выражения.

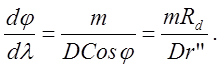                                                                                           (7)

Угловая дисперсия минимальна при наблюдении спектра по нормали к ДР. В спектрографах светочувствительная поверхность фотопленки совмещается с кругом Роуланда, который является линией дисперсии. Линейная дисперсия вогнутой ДР определяется вдоль круга Роуланда:

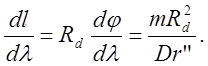                                                                                                  (8)

Разрешающая способность вогнутой ДР определяется также как и плоской. Однако для вогнутой ДР имеется ограничение на размер решетки  Поскольку с увеличением размера ДР все больше отклоняется от круга Роулана. В результате для лучей, дифрагированных от концов решетки возникает дополнительная разность хода, которая согласно условию Рэлея не должна превышать λ/4 (что отвечает моменту расфазировки интерферирующих лучей).

Ошибки в работе делительной машины при нарезании решеток приводят к появлению в спектре ложных спектральных линий – духов. Периодические ошибки нарушения периода (духи Роуланда если ошибка возникает через несколько сот штрихов, духи Лаймана  - если период ошибки несколько штрихов) решетки можно рассматривать как совокупную картину дифракции от двух типов решеток. Яркость духов пропорциональна квадрату порядка спектра. Духи определяются по изменению их яркости при диафрагмировании части решетки.