Временная и пространственная когерентность

Лекция №9

Временная и пространственная когерентность

очень важной характеристикой источника света является его временная и пространственная когерентность. Чтобы разобрать эти явления рассмотрим сначала источник квазимонохроматического излучения, состоящий из двух точечных источников s1 и s2 (например, атомов). Пусть атомы излучают свет – плоские волны независимо (отсутствуют кооперативные эффекты) и поляризацию излучения будем считать одинаковой и линейной. Фотоприемник в точке p зарегистрирует средний квадрат напряженности поля. Особенности явления, о котором пойдет речь в равной мере относятся к освещенности, яркости, световому потоку – к любой фотометрической величине. Конкретная величина зависит от типа фотоприемника. Мы будем пользоваться термином интенсивность – квадратом модуля напряженности электрического поля.

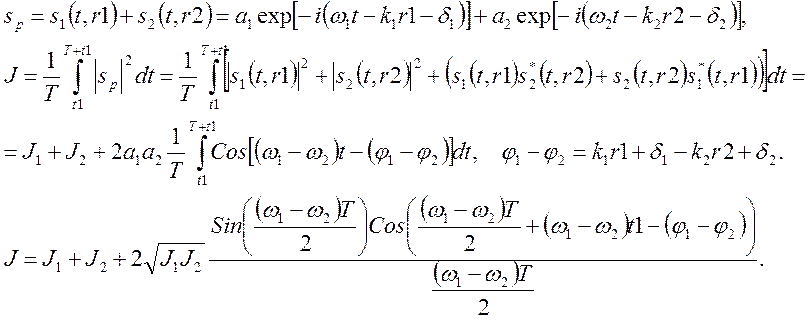                                                                                                                             (9.1)

В (9.1) время T – постоянная времени фотоприемника. Если разность частот не очень велика и разность фаз φ₁-φ₂ постоянна в течение времени регистрации T, то третье интерференционное слагаемое в (9.1) не равно нулю. Наблюдаются биения – переменный сигнал с разностной частотой ω₁-ω₂.  Тогда считается, что источники s₁ и s₂ когерентны в течении времени T. Из формулы (9.1) следует, что  результат не зависит от начала отсчета времени t1, что характеризует процесс излучения как стационарный. В выражениях (9.1) третье слагаемое можно переписать в терминах временных задержек, поскольку общее решение волнового уравнения есть функция от аргумента ωt-kr=ω(t-τ), k=ω/c, τ=r/c:

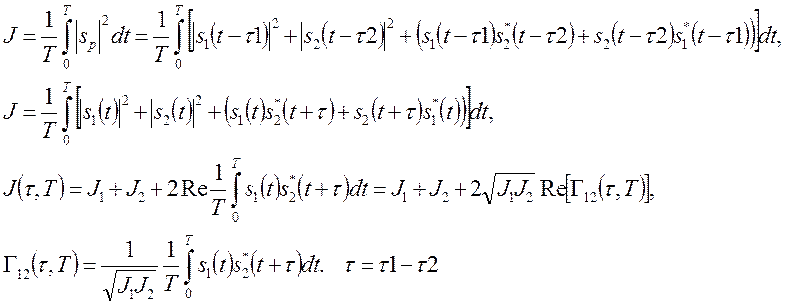(9.2)

При T>>τ можно считать, что интеграл берется от нуля до  бесконечности и Г₁₂(Т,τ)→ Г₁₂(τ) - становится функцией корреляции. В (9.2) сдвиги переменной интегрирования возможны поскольку процесс излучения источниками s1 и s2 считается стационарным. Для полностью когерентных источников и бесконечном времени наблюдения частоты источников должны быть равными и интенсивность в точке наблюдения задается разностью фаз или разностью хода (Г₁₂(τ)=exp(iψ)=exp(i(φ₁-φ₂))). При этом модуль функции корреляции равен 1. При неполной когерентности функция корреляции изменяется от нуля до единицы. Значение модуля функции корреляции определяет диапазон изменения интенсивности в точке регистрации:

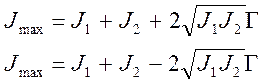                                                                                          (9.3)

Максимальное и минимальное значение интенсивности возникающее при изменении положений источников или места регистрации и регистрируемое фотоприемником, характеризуют функцию видности интерференционной картины:

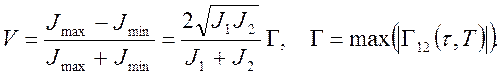                                          (9.4)

Можно определить функцию корреляции для одного источника, но двух пучков, считая, что τ – задержка распространения света в двух пучках. Тогда функция взаимной корреляции Г₁₂(τ) перейдет в функцию автокорреляции Г₁₁(τ), которая характеризует «сфазированность» колебании одного и того же источника в разные моменты времени. Качественно понятие когерентности можно определить как необходимую стабильность случайных фазовых соотношений между волнами за время измерения интерференционной картины. Г(τ)=Г(r₁,t₁,r₂,t₂) задает степень когерентности полей в пространственно-временных точках r₁,t₁ и r₂,t₂. Масштаб τ, на котором в определенной мере спадает функция корреляции |Г(r₁,t,r₁,t+τ)| называется временной когерентностью. Длина L=cτ называется длиной когерентности (продольный размер когерентности). При разнесении точек наблюдения поперек направления распространения светового пучка функция корреляции |Г(r₁,t₁,r₂,t₂)| также будет убывать. Характерный масштаб спадания функции при разнесении точек источника от оси называется поперечным радиусом когерентности. Он характеризует размер участков волнового фронта, от которых может быть получена четкая интерференционная картина. Площадка когерентности – это участок экрана, перпендикулярный пучку, внутри которого |Г(r₁,t₁,r₂,t₂)|  не падает меньше заданной величины. Для удаленного квазимонохроматического источника, все элементы которого излучают независимо, функция корреляции дается пространственным Фурье образом распределения интенсивности по площади источника. Например, для плоского диска постоянной светимости вид корреляционной функции таков:

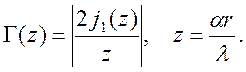                                                              (9.5)

j₁(z) – функция Бесселя первого рода, α – угловой размер источника, r – расстояние между точками 1 и 2. Первый нуль (9.5) – при значении z=3.83. Временем когерентности называется минимальная задержка τ, снижающая Г(τ) до заданной величины (в e-раз или до нуля). Зависимость Г(τ)  дается спектром мощности поля:

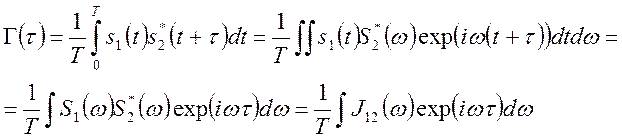                                                    (9.6)

В формуле (9.6) параметр T – это время наблюдения спектра источника. Если характерные времена всех процессов в источнике много меньше T, то (9.6) от времени наблюдения не зависит.

Проследим несколько конкретных примеров между спектром источника и видом функции автокорреляции.

Первая модель – это монохроматический источник J(ω)= δ(ω-ω₀). Тогда функция корреляции Г(τ)=exp(iω₀τ) и модуль функции корреляции всегда равен единице. Интерференционная картина будет контрастной при любой разности хода и временной задержке между волнами.