ЛЕКЦИЯ
Диспергирующие элементы спектральных приборов. дифракционная решетка.
Диспергирующим элементом в дифракционных спектральных приборах служит дифракционная решетка (ДР). Оптическая поверхность из металла или прозрачного материала, на которую нанесены штрихи, определенным образом разбивающие фронт падающей световой волны на отдельные когерентные пучки с измененной амплитудой или фазой. Интерференция набора этих пучков перераспределяет энергию излучения в пространстве и определяет спектроскопические характеристики прибора. Форма штриха может быть любой. Важно, чтобы одинаковые штрихи повторялись строго через одинаковые промежутки – период дифракционной решетки. Т.о. нарезные дифракционные решетки (или копии с них – реплики) представляют собой одномерную периодическую структуру. В последнее время наибольшее распространение получили голографические дифракционные решетки. Существуют отражательные и прозрачные дифракционные решетки (деление по месту получения дифракционной картины в отраженном свете или в прошедшем). Если штрихи нанесены на плоскую поверхность – плоские решетки, если на вогнутую сферическую – вогнутые с фокусирующим действием.
 Плоская
дифракционная решетка. Общая теория плоской ДР создана Роуландом в 1893 году. (Rouland H. Gratings in Theory and Practice
. Phil. Mag. 1893, v.35. p.397.). Пусть
на отражательную решетку с периодом D падает
световая волна. Каждая точка ДР (принцип Гюйгенса-Френеля) становиться
источником вторичных волн. Результирующее поле – это сумма всех вторичных волн.
Поскольку ДР имеет конечный размер и камерный объектив отображает ДР на
бесконечность, буде искать распределение светового поля в приближении дифракции
фраунгофера. Колиматорный
объектив также отображает источник света на бесконечность, поэтому можно
считать падающую световую волну плоской. Выберем систему координат: ось z - в
направлении штриха, ось y – в плоскости решетки и перпендикулярно штриху. Пусть
источник находится в точке с координатами x’,y’,z’.
Световая монохроматическая волна, излучаемая источником описывается выражением:
Плоская
дифракционная решетка. Общая теория плоской ДР создана Роуландом в 1893 году. (Rouland H. Gratings in Theory and Practice
. Phil. Mag. 1893, v.35. p.397.). Пусть
на отражательную решетку с периодом D падает
световая волна. Каждая точка ДР (принцип Гюйгенса-Френеля) становиться
источником вторичных волн. Результирующее поле – это сумма всех вторичных волн.
Поскольку ДР имеет конечный размер и камерный объектив отображает ДР на
бесконечность, буде искать распределение светового поля в приближении дифракции
фраунгофера. Колиматорный
объектив также отображает источник света на бесконечность, поэтому можно
считать падающую световую волну плоской. Выберем систему координат: ось z - в
направлении штриха, ось y – в плоскости решетки и перпендикулярно штриху. Пусть
источник находится в точке с координатами x’,y’,z’.
Световая монохроматическая волна, излучаемая источником описывается выражением:
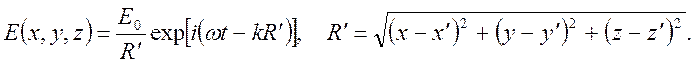 (1)
(1)
В точке наблюдения поле является суммой всех вторичных источников:
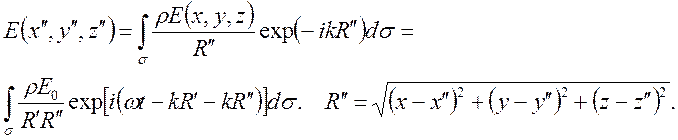 (2)
(2)
Интеграл берется по поверхности решетки, r - коэффициент отражения. По условию задачи r’ >> r и r” >> r. Разложим расстояния от точки наблюдения до ДР и от источника до ДР.
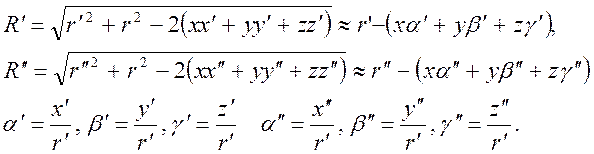 (3)
(3)
В (3) мы пренебрегли слагаемыми r2/r’, величины a’,b’,g’ и a”,b”,g” - направляющие косинусы на источник и точку наблюдения. Произведение R’R” в формуле (2) в приближении дифракции Фраунгофера сводится к произведению r’r” (зависимость от точки интегрирования приводит к слабой модуляции яркости вторичных источников, она учитывается в случае вогнутых решеток). Интенсивность излучения в точке наблюдения дается выражением:
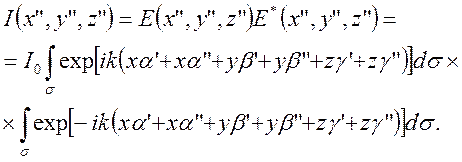 (4)
(4)
 Перейдем от направляющих косинусов к
полярным и азимутальным углам в системах координат входной и выходной щелей. Поскольку
после коллиматорного объектива и перед камерным объективом излучение – это
плоская волна, вместо направляющих косинусов в полярных координатах можно
написать:
Перейдем от направляющих косинусов к
полярным и азимутальным углам в системах координат входной и выходной щелей. Поскольку
после коллиматорного объектива и перед камерным объективом излучение – это
плоская волна, вместо направляющих косинусов в полярных координатах можно
написать:
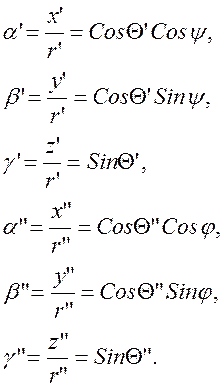 (5)
(5)
Будем считать, что дифракция идет настрого периодической структуре. Тогда интеграл по поверхности решетки можно разбить на интеграл по оси z и на интеграл по ломаной линии в плоскости xy (по профилю решетки):
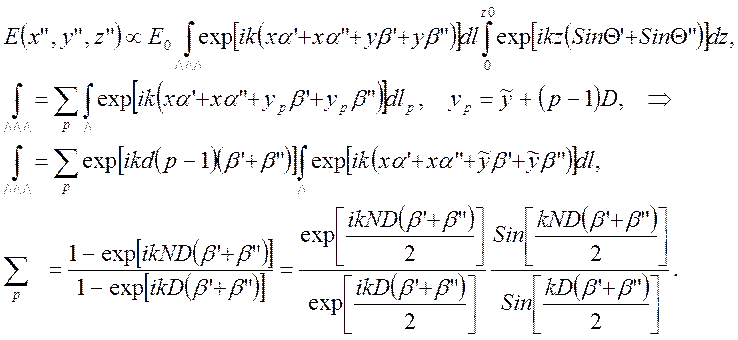 (6)
(6)
Без конкретизации формы штриха ДР найдем распределение интенсивности в точке наблюдения:
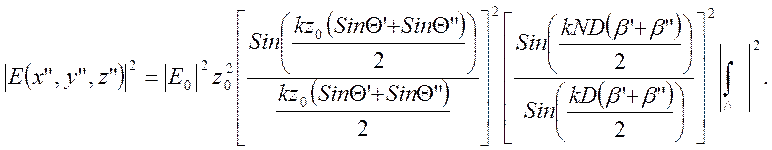 (7)
(7)
Первый множитель в (7), зависящий от высоты решетки z0, - это известная дифракционная функция (дифракция на щелевом отверстии). Направление на центральный максимум определяется значением аргумента синуса, равным нулю:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.