(8)
Т.е. направление на центральный максимум в плоскости, параллельной штрихам, определяется законом зеркального отражения. Угловая ширина – т.е. расстояние между максимумом и первым нулем задается аргументом синуса равным p:
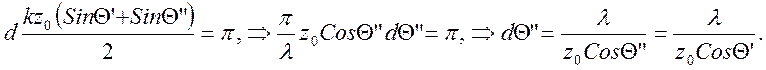(9)
При условии большой ДР - z0>>lширина главного максимума мала - DQ”f2<<h2 и размытием точки входной щели в плоскости выходной щели вдоль щели можно пренебречь.
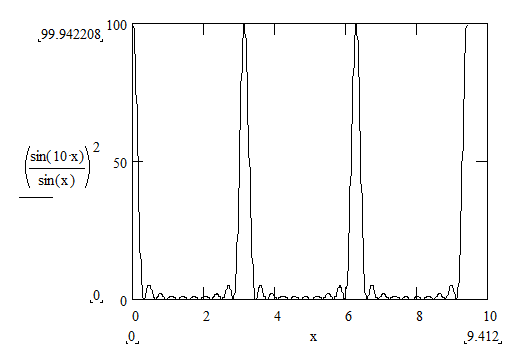Распределение интенсивности в
плоскости дисперсии (перпендикулярно штрихам) задается остальными множителями
(вторым и третьим) в формуле (7). Второй множитель (7) целиком обусловлен
периодичностью решетки и зависит от периода D,
числа штрихов N и углов падения и рассеяния:
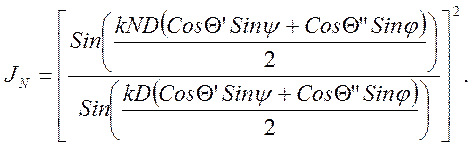(10)
JN – периодическая функция с главными и второстепенными максимумами. Амплитуда главных максимумов равна N2, когда синус в знаменателе обращается в ноль (числитель тоже тогда равен нулю).
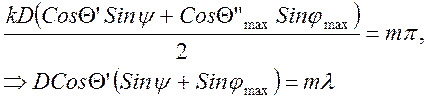(11)
Следовательно при заданных углах Q’ и y и постоянном m угол дифракции однозначно определяется длиной волны l. Т.е. направление на главные максимумы для разных длин волн различны и ДР осуществляет угловое разложение излучения по длинам волн (в спектр). Однако для каждой длины волны существует несколько главных максимумов, отвечающих разному значению m. Т.е. образуется несколько пространственных разложений спектра, свое для каждого значения m, определяющего порядок спектра. При m=1 образуется спектр 1-го порядка, при m=2 – второго и т.д. Нули JN определяются обращением в ноль числителя при знаменателе не равном нулю. Между главными максимумами находится N-1 нулей. Побочные максимумы (N-2 максимума) лежат приблизительно между нулями. Функция JN является аппаратной функцией. При m=0 положение главного максимума (j0max=-y) не зависит от длины волны – это ахроматический максимум, определяемый зеркальным отражением. В нулевом порядке не происходит разложения излучения в спектр. Легко видеть, что величина D=D(Siny+Sinj) представляет собой геометрическую разность хода для двух параллельных лучей, точки падения которых на решетку отстоят на период решетки - D(разность хода от двух соседних штрихов). Если падающий и дифрагированный лучи находятся по одну сторону от нормали в выражении для разности хода угол j следует заменить на -j. Из (11) следует, что если в каком-то направлении разность хода между лучами, дифрагированными от соседних штрихов ДР, равна целому числу длин волн - m, то это есть направление на главный максимум порядок которого равен m.
Угловая дисперсия ДР получается дифференцированием (11):
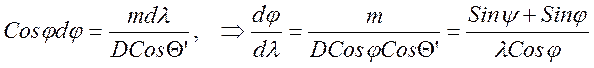(12)
Угловая дисперсия решетки увеличивается с уменьшением периода решетки и с увеличением отклонения дифрагированного луча от направления зеркального отражения. В ряде случаев удобно использовать решетку в области малых углов дифракции j=0 и произвольных углов падения. В этом случае угловая дисперсия слабо зависит от угла дифракции и практически постоянна. Тогда для разложения выходного излучения в спектр на выходе прибора можно применять линейную интерполяцию (так называемый нормальный спектр при нормальном угле дифракции).
Разрешающая способность дифракционной решетки определяется аппаратной функцией JN (10) – ширинами главных максимумов – фактически берется расстояние между максимумом и нулем:
(13)
Продифференцируем равенство (13):
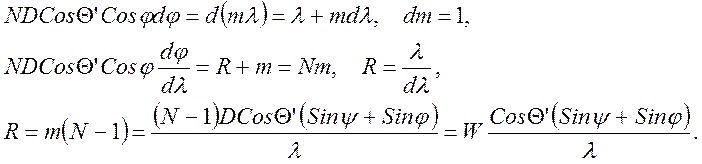(14)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.