Вторая модель – модель осцилляторов Лоренца, когда «монохроматическое» (синусоидальное) излучение постоянной амплитуды существует в течениие какого-то времени:
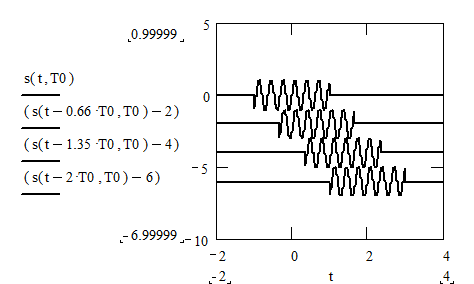
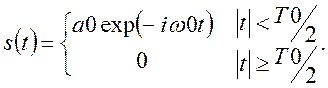(9.7)
На рисунке показаны цуги излучения испущенные в разные моменты времени. Спектр такого источника определяется преобразованием Фурье:
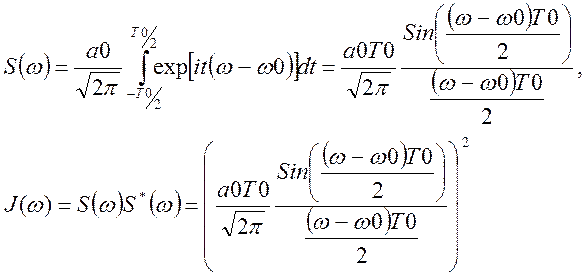(9.8)
Ширина спектра Δω=2π/T0 определяется временем излучения цуга волн. Соответствующая функция корреляции дается выражением:
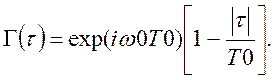(9.9)
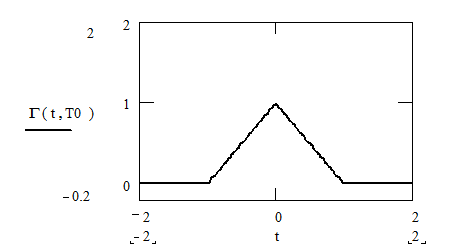
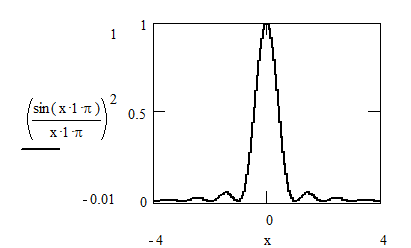Не трудно убедиться, что фурье-образ функции (9.9) корреляции
соответствует спектру (9.8).
Нетрудно понять, что функция корреляции осцилляторов Лоренца Г(τ) соответствует площади перекрытия цугов источника, задержанных на время τ.
Третья модель – набор волновых цугов с произвольной фазой и случайной длительностью. Эта модель отвечает излучению атома (осциллятора), подвергающегося столкновениям, которые сбивают фазу излученного цуга. За время свободного пробега атом излучает синусоидальную волну, в момент столкновения фаза волны меняется случайным образом. Согласно кинетической теории, вероятность того, что время свободного пробега лежит в интервале от T0 до T0+dT0 дается распределением Пуассона:
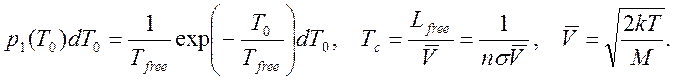(9.10)
Фаза излучения после одного столкновения меняется случайным образом, поэтому интерферировать могут волновые цуги лишь сами с собой. Спектр такого процесса есть результат суммирования спектров (9.8) по всем возможным длинам цугов с распределением (9.10). Поскольку преобразование Фурье – линейное преобразование, суммирование можно провести сразу с функцией корреляции:
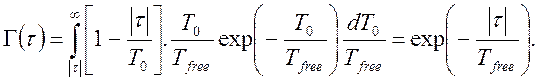(9.11)
В (9.11) учтены цуги с длительностью T0 больше, чем τ (в противном случае функция корреляции отдельного излучателя Лоренца равна нулю). Второй множитель – это относительное число цугов, длительность которых лежит в интервале T0 до T0+dT0. Последний множитель – это вероятность того, что длительность цуга лежит в интервале T0 до T0+dT0.
Для доплеровского контура спектр излучения задается функцией Гаусса:
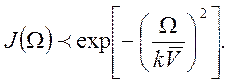(9.12)
Функция корреляции такого источника, фурье-образ будет следующей (фурье-образ функции Гаусса – функция Гаусса):
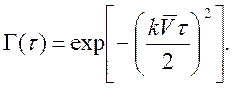(9.12)
Экспоненциально затухающие колебания, которым соответствует спектр, описываемый функцией Лоренца обладают также экспоненциальной функцией корреляции:
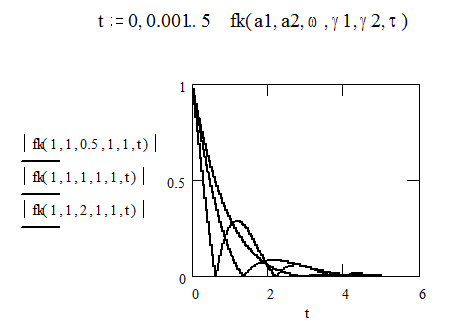
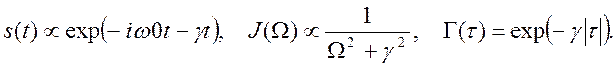(9.13)
На рис. приведены корреляционные функции бихроматического источника при различном частотном расщеплении. При слабом расщеплении поведение корреляционной функции похоже на (9.13). При увеличении частотной отстройки возникают все более заметные биения. Во всех рассмотренных случаях скорость уменьшения корреляционной функции определяется спектральной шириной источника. Т.е. можно наблюдать интерференционную картину от точечного источника при внесении такой задержки τ между интерферирующими лучами, чтобы корреляционная функция не уменьшилась больше заданных пределов. Этой задержке отвечает разность хода сτ.
Рассмотрим формирование интерференционной картины (ИК) от монохроматического, но протяженного источника. В этом случае для формирования ИК важной характеристикой источника является его пространственная когерентность. Чтобы понять суть этого термина обратимся к интерференционной схеме с бипризмой Френеля. Т.е. имеем источник с размером d. Излучение проходит через бипризму Френеля, получаем два фиктивных источника разнесенных на расстояние D. Сопряженные точки обоих источников попарно когерентны. Произвольные пары точек дают некогерентное излучение. Каждая пара сопряженных точек дает свою интерференционную картину. Для крайних пар точек источников ИК сдвинуты на расстояние d. Если этот сдвиг окажется равным расстоянию между максимумом и минимумом индивидуальной ИК, то суммарная ИК замоется. Расстояние между максимумом и минимумом ИК легко вычислить, найдя изменение разности хода при смещении точки наблюдения на экране:
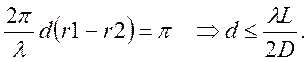(9.14)
При выполнении соотношения (9.14) можно считать, что крайние точки источника излучают сфазированно. Источники можно разнести на минимальное расстояние D=d, тогда получим характерный размер площадки когерентности:
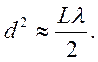(9.15)
Для объемного источника диаметром d и длиной L, то излучение в конусе углов d/L=λ/d также будет сфазаровано. Т.е. зона когерентности определяется из равенства геометрической и дифракционной расходимости. Формула (9.15) также гласит, что зона когерентности расширяется с увеличением расстояния до источника. В общем случае зона когерентности определяется Фурье-образом пространственного распределения мощности излучения. Для светящейся полоски пространственная функция корреляции дается выражением:
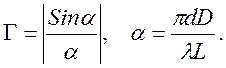(9.16)
Формулу (9.16) можно получить простым суммированием излучения от каждой точки протяженного источника на экране.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.