Аберрации оптических систем. Хроматическая аберрация

ЛЕКЦИЯ

 аберрации оптических систем

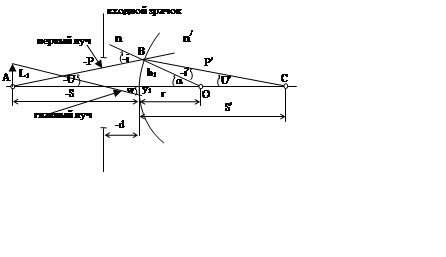Для приблизительного вычисления остальных аберраций используются два параксиальных луча. Первый луч, проходящий через точки оптической оси в местах расположения изображений предмета и главный луч, проходящий через крайние точки предмета и центры изображений входного зрачка. Пересечение главного луча с оптической осью дает положение изображений входного зрачка. Для изображений входного зрачка также можно ввести нуль инварианты, как и для предмета.

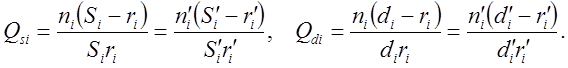                               (1)

Для первого луча высоты пересечения с преломляющей сферической поверхностью - h_i для главного луча соответственно - высоты пересечения с преломляющей сферической поверхностью -y_i. Через эти параметры записываются остальные суммы Зайделя. Всего их пять и через значения этих сумм вычисляются все аберрации оптических систем со сферическими преломляющими поверхностями (стр.296 Б.В.Фефилов «Прикладная оптика» М.1947г.):

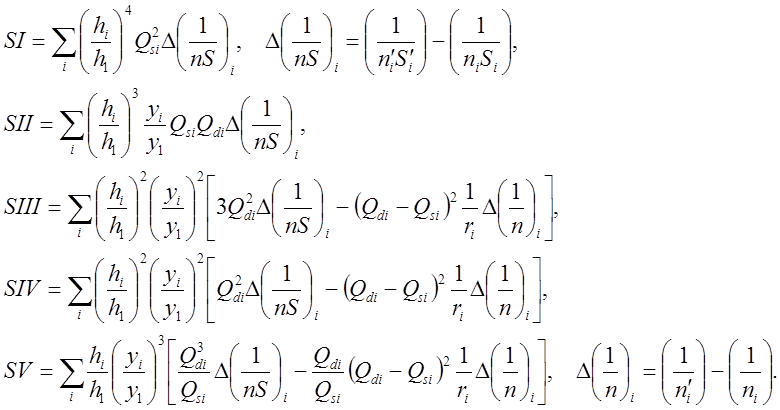  (2)

Рассмотрим теперь величины аберраций различных типов, выраженные через суммы Зайделя. Выразим значения аберраций через высоты лучей – ξ || оси x и η || оси y в плоскости входного зрачка.

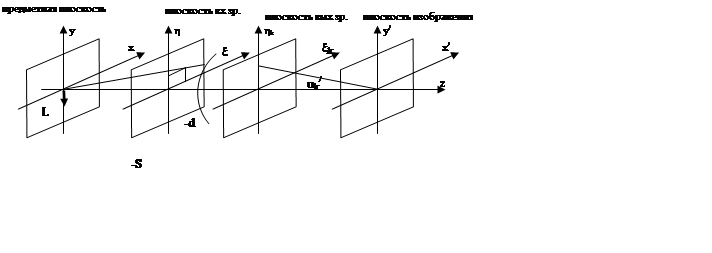Для сферической аберрации (точка предмета расположена на оси), выраженной через параметры луча на входном зрачке, можно получить следующие выражения.

(3)

Если точка предмета расположена вне оси, то помимо сферической аберрации возникают другие искажения. Для случая чистой меридиональной комы можно получить выражения для уклонения луча от параксиальной траектории:

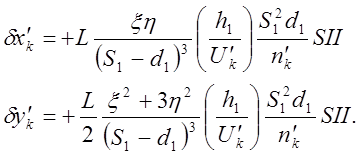                                                           (4)

Форма аберрационной кривой, как уже рассматривалось ранее, - семейство окружностей с радиусом и положением центра (стр.302 Б.В.Фефилов «Прикладная оптика» М.1947г.):

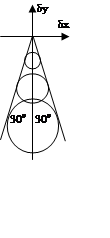
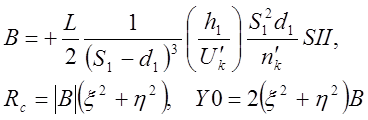                            .     (5)

В случае чистой комы вместо точки имеет место пятно кометообразной формы с резко выраженным хвостом. Направление хвоста зависит от знака B. Касательные к окружностям, отвечающим увеличению радиуса входного зрачка составляют с осью Y углы в 30⁰.

Третья и четвертая суммы Зайделя задают отклонение параксиального фокуса от точки пресечения меридионального и сагиттального пучка лучей  и связаны с астигматизмом (стр.304):

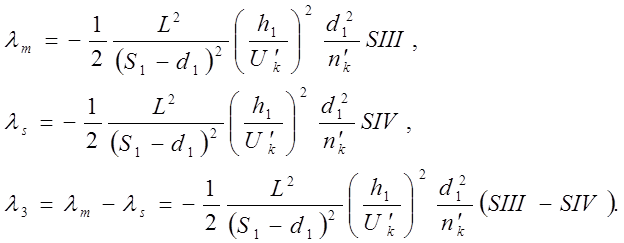                            (6)

λ₃ – есть астигматическая разность, следовательно разность SIII-SIV – служит мерой астигматической ошибки.

Уклонение траектории главного луча от парксиальной приводит к другой точке пересечения с гауссовой плоскостью. Отклонение задается пятой суммой Зайделя:

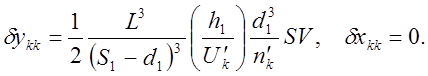                                                     (7)

Более простой критерий для получения изображения хорошего качества – это уничтожение сферической аберрации для центра объекта и выполнение закона синусов для всего отверстия  (широкоугольное выражение для  инварианта Лагранжа-Гельмгольца):

                                                                                     (8)

При этом не нарушается структура пучка.

Хроматическая аберрация. Поскольку показатель преломления всех существующих материалов в той или иной степени зависит от длины волны света, то линзы обладают хроматической аберрацией уже в параксиальном приближении. Действие хроматической аберрации сводится к тому, что фокусное расстояние элементов оптической системы начинает зависеть от длины волны.  При освещении оптической системы немонохроматическим светом свет с разными длина ми вол будет фокусироваться в разных пространственных точках.

Найдем изменение нуль инварианта при изменении показателя преломления:

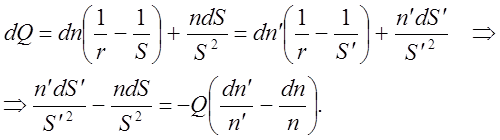                                            (9)

Умножим обе части (9) на h² чтобы в дальнейшем перейти к углам и просуммируем (9) по всем поверхностям учитывая равенство углов и показателей преломления как это делалось для серической аберрации. Полагая начальный объект реальным и безаберрационным окончательно получим:

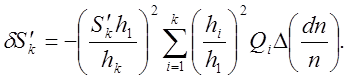                                                                   (10)

Выражение под знаком суммы носит название первой хроматической суммы. Подбор оптических материалов и положения сферических поверхностей с целью обращения первой хроматической суммы в ноль называется ахроматизацией. Для системы тонких линз в воздухе формула (10) может быть приведена к виду:

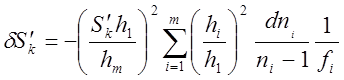                                                                    (11)

 Величину (n-1)/dn=ν – называют числом Аббе. В области нормальной дисперсии для собирающей линзы синий фокус ближе красного (недоисправлена хроматическая аберрация). Для рассеивающей линзы наоборот синий фокус дальше красного (переисправлена). Исправление хроматической аберрации для склейки линз из одного материала невозможно. Для склеек из разных сортов стекла возможно исправление хроматической аберрации. Система тонких линз на расстоянии может быть ахроматизирована. Показать.