Новосибирский государственный университет
Факультет естественных наук
Кафедра физической химии
Выполнили:
Семионова В.В.
Стрижаков Р.К.
гр. 742
Преподаватель:
Арзуманов С.С.
Новосибирск, 2009
Для двухатомной молекулы положение центра полосы в колебательно-вращательном спектре дает частоту колебаний молекулы, а расстояния между линиями вращательной структуры позволяет определить момент инерции молекулы. Эти сведения позволяют рассчитать статистическую сумму, знание которой позволяет вычислить все термодинамические характеристики.
Статистическая сумма - это одно из важнейших понятий статистической физики. Она равна общему числу состояний, в которых может находиться система при данной температуре.
,
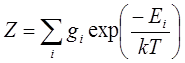где gi - кратность вырождения i - го состояния.
Суммарную энергию, которой обладают молекулы газообразного вещества, можно разделить на поступательную и внутримолекулярную. Последняя в свою очередь может быть представлена как сумма энергий трех видов движений: электронного, колебательного и вращательного.
Е = Епост + Еэл + Екол + Евращ
Такое разделение энергии молекулы является хотя и приближенным, но достаточно точным. При необходимости можно ввести поправки соответствующие энергиям взаимодействия различных видов движения:
Е = Епост + Еэл + Екол + Евращ Еэл.кол + Екол.вращ + Еэл.вращ
Существенно, что при определенных условиях Еэл. кол можно включить в Екол, а Екол в Евращ., тогда разделение энергии на три вклада остается справедливым и при учете взаимодействий.
Подобно тому, как полная энергия молекулы может быть распределена между отдельными ее видами: поступательной, вращательной, колебательной и электронной, статсумма молекулы может быть представлена произведением статсумм, соответствующих отдельным типам движения:
Z = Zпост·Zэл·Zкол·Zвращ
Если система состоит из N неразличимых невзаимодействующих частиц, полная статистическая сумма Z определяется через статсумму одной частицы Z1 следующим образом:
.
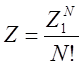1. Поступательная статсумма молекулы.
Для поступательного движения число доступных состояний всегда очень велико и сумма по состояниям может быть заменена интегралом по фазовому объему. Для данной молекулы фазовый объем является шестимерным. Окончательный вид после интегрирования формулы для вычисления поступательной статсуммы:
,
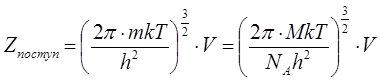где V – объем, в котором находиться молекула (м3); m – масса молекулы (кг); М –молекулярная масса (кг/моль); Na – число Авогадро; h – постоянная Больцмана; Т –температура.
2. Вращательная статсумма.
Молекула называется жесткой, если ее моменты инерции не зависят от ее энергетического состояния. Для жестких линейных молекул при достаточно высоких температурах, когда сумму по состояниям можно заменить интегралом по состояниям, выражение для Zвpaщ имеет вид:
,
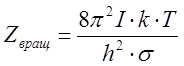где I – момент инерции молекулы (кг-м2), σ – число симметрии. Число симметрии равно числу поворотов, которое совмещают молекулу саму с собой. При этом отражения, зеркальные повороты и инверсия не рассматриваются, поворот на 360 градусов учитывается один раз. Для симметричных линейных молекул число а = 2, для линейных несимметричных молекул число о = 1 (например, для СО).
3. Колебательная статсумма
В случае квантового гармонического осциллятора колебательная статсумма, определяется как:
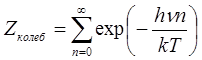, где n = 0, 1, 2,...; Ео
=
– начало отчета.
Видно, что выражение для Zколеб является убывающей геометрической прогрессией. Поэтому выражение для Zколеб гармонического осциллятора имеет вид:
,
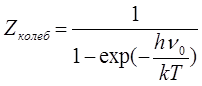где ν – частота колебаний, которая определяется из вращательно-колебательных спектров молекулы.
Если в молекуле имеется несколько колебаний, то колебательная статсумма представляет собой произведение колебательных статсумм с учетом выраждения:
, где ni - вырождение i-гo колебания.
Свободная энергия Гельмгольца.
.
В случае N независимых, невзаимодействующих и одинаковых частиц:
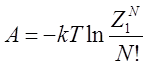
Или, используя формулу Стирлинга:
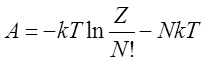, для одного моля вещества Nk = NAk = R.
Энтропия.
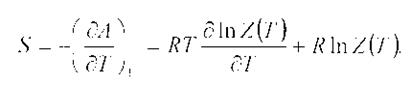
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.