Вращательные и колебательные спектры двухатомных молекул, страница 3

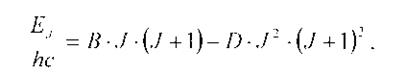
где D – постоянная центробежного растяжения. Для нежесткого ротатора линии вращательной структуры в Р-ветви расходятся с ростом J, а линии в R-ветви сближаются.

Для определения вращательных постоянных из колебательно-вращательных спектров используют так называемые комбинационные разности Δ₂F, которые представляют собой разность между уровнями вращательной энергии двух вращательных состояний, расположенных через один вращательный уровень:

Δ₂F(J) = R(J) – P(J) = R(J - 1) – P(J + 1).

Здесь R(J) и P(J) – линии R- и Р-ветвей соответственно. Для жесткого ротатора

Δ₂F(J) = 4B·(J + 1/2).

Экспериментальная часть

Цель работы: записать хорошо разрешенный спектр исследуемого газа (СО) в той области волновых чисел, где наблюдается поглощение. Определить по спектру вращательную постоянную В, момент инерции исследуемых молекул. Рассчитать термодинамические параметры исследуемых веществ.

Из записанного спектра для СО определили следующие параметры: J,  = R(J)– P(J), а также (J + ½)² и ∆₂F(J)/(J + ½):

J	∆2F(J)	(J + ½)2	∆2F(J)/(J + ½)
1	11,8	2,25	7,87
2	19,6	6,25	7,84
3	27,4	12,25	7,83
4	35,3	20,25	7,84
5	42,5	30,25	7,73
6	50,3	42,25	7,74
7	58,2	56,25	7,76
8	65,5	72,25	7,71
9	73,0	90,25	7,68
10	81,0	110,25	7,71

Построили график зависимости ∆₂F(J)/(J + ½) от (J+ ½)², имеющий вид ∆₂F(J)/(J + ½) = 4В – 8D∙(J + ½)², с использованием программы Origin. Методом наименьших квадратов рассчитали вращательную постоянную В, В = 1,9600 ± 0,0048 cм^-1 (196 м-1)

По формуле 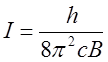 рассчитали момент инерции молекул СО:

.

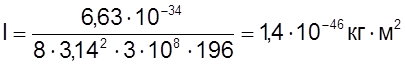Из справочных данных:

Рассчитали статсумму: Z = Z_вращZ_колебZ_поступZ_эл.

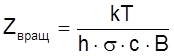, где Т = 298К, σ = 1.

.

,

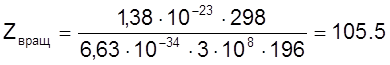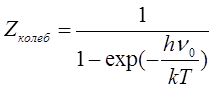из спектра нашли, что 2147 см^-1 (колебательный переход) соответствует .

.

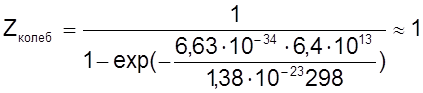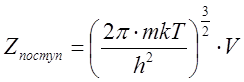, где V = 22,4 л/моль, . .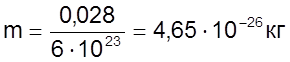

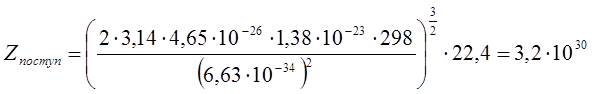Тогда получаем, что .

Зная значение статсуммы, получили значения термодинамических параметров.

Рассчитали, используя выше приведенные формулы, свободную энергию Гельмгольца:

 кДж/моль.

Рассчитали энтропию, учитывая, что S = S_колеб + S_вращ + S_пост.

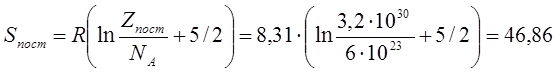Дж/моль·К, Дж/моль·К, ,

.

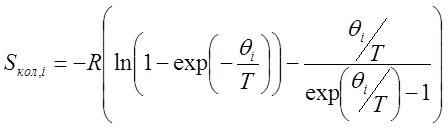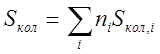Из спектра нашли 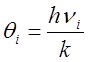. По спектру θ₀ = hυ₀/k. Больше никаких колебательных линий в спектре нет. Тогда по спектру находим, что υ₀ = 6,4∙10¹³ Гц. Тогда θ₀ = 3091 К. Зная эту величину и используя приведенное выше выражение, найдем S_кол. Оно равно 2,995∙10^-3 Дж/моль·К. В итоге получаем, что общая энтропия S = 196,36 Дж/моль∙К. Также для данного соединения можно найти внутреннюю энергию колебательного, вращательного и поступательного движения.

U_пост = 3/2·RT

U_вращ = RT (так как молекула линейная)

U_кол = R· [ θ₀/(1-exp(-θ₀/T))]

Они равны соответственно 3,71,  2,48 и 256,89 кДж/моль. Далее можно найти другие термодинамические функции:

H_пост  = 5/2·RT = 6190.95 Дж/моль

G_пост  = A_пост + RT =  -7764.68 Дж/моль

H_вращ = U_вращ = 2,47 кДж/моль

G_вращ = A_вращ = -R∙T∙lnZ_вращ = -11,54 кДж/моль

H_кол = U_кол  = 25688.5 Дж/моль

G_кол = A_кол  = -RTlnZ_кол ≈ 0 Дж/моль

Для системы можно рассчитать:

C_v = 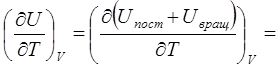 2RT(∂ln(Z(T))/∂T)+RT²·∂/∂T(∂ln(Z(T))/∂T) + R

и оно равно:

C_v = 3R - 3/2·R + R = 5/2·R = 20.775 Дж/моль·К.

При условии, что температуры не высокие и колебательная степень свободы еще не разморожена.

Выводы:

·  Провели запись обзорных спектров в широкой области волновых чисел; определили область, в которой наблюдается поглощение;

·  Записали с хорошим разрешением исследуемого газа в той области волновых чисел, где наблюдается поглощение. После регистрации спектра сделали несколько отметок волновых чисел на спектре, что дало возможность для построения шкалы волновых чисел;

·  Обработали спектры методом комбинационных разностей и определили вращательную постоянную В;

·  Определили моменты инерции исследуемой молекулы;

·  Рассчитали термодинамические параметры исследуемого газа.