Вращательные и колебательные спектры двухатомных молекул, страница 2

Для моля вещества, состоящего из линейных молекул, поступательная и вращательная составляющие энтропии S_пост и S_вp  равны:

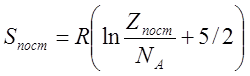
Колебательная составляющая энтропии, соответствующая i-му колебанию, равна:

,

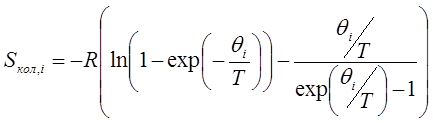где θ_i - характеристическая колебательная температура .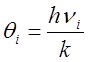

Полная  вращательная  энтропия  определяется  как  сумма  по   всем   колебаниям молекулы с учетом вырождения:

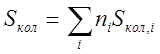, где n_i - вырождение i-ro колебания.

Внутренняя энергия.

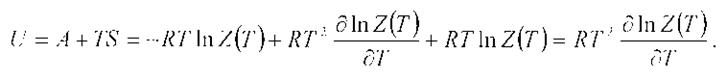
Эту формулу также можно применить к отдельным видам молекулярного движения:

U_пост = (3/2)RT.

При Т>>θ_вращ получаем:

U_вращ = RT (для линейных молекул) и

U_вращ = (3/2)RT (для нелинейных молекул).

.

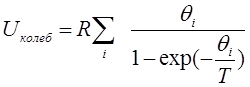Выражения для Н и G:

H_пост = U_пост + pV = (5/2)RT,

Н_вращ = U_вращ,

Н_кол = U_кол,

G_пост = А_пост + pV = А_пост + RT,

G_вращ = A_вращ

G_кол = A_кол

Теплоемкость.

Вращательные и колебательные спектры молекул.

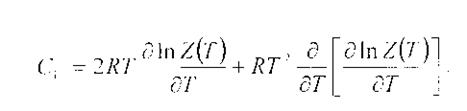
Спектры молекул, в отличие от линейных спектров атомов, состоят из широких полос, которые иногда распадаются на отдельные тесно расположенные лини. Вращательным спектрам поглощения соответствуют волновые числа 1-50 см^-1 и меньше, т.е. эти спектры лежат в далекой ИК области и в области радиочастот. В колебательных спектрах молекул основные переходы расположены в области 100-4000 см^-1, поскольку вместе с колебаниями возбуждаются и вращения молекул, фактически в этой спектральной области наблюдаются не чисто колебательные, колебательно-вращательные спектры.

Решение уравнения Шредингера дает следующее выражение для термов вращательной энергии жесткой двухатомной молекулы:

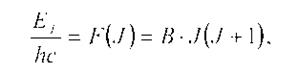
где В – вращательная постоянная, J – вращательное квантовое число, принимающее значение 0, 1,2...

Выражение для термов колебательной энергии двухатомной молекулы в приближении гармонического осциллятора имеет вид:

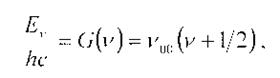
где ν₀₀ - расстояние между соседними колебательными уровнями энергии (см^-1), ν –колебательное квантовое число.

Термы колебательно-вращательных состояний являются суммой колебательной и вращательной составляющих:

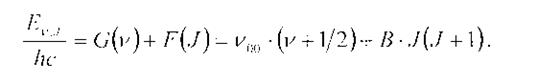
Рассмотрим вращательную структуру колебательно-вращательных ИК-спектров. В соответствии с правилом отбора ΔJ = ± 1 осуществляются 2 серии переходов между вращательными состояниями разных колебательных уровней. Поэтому в спектре, соответствующему одному колебательному переходу, наблюдается 2 серии линий, которые называют ветвями полосы: серия линий называется R-ветвью, если ΔJ = +1 и Р-ветвью, если ΔJ = -1. Между R- и Р-ветвями находится так называемый нулевой промежуток ν₀₀, который соответствует чисто колебательному переходу, запрещенному по правилам отбора для большинства двухатомных молекул. Переход, при котором ΔJ = 0, – это Q-ветвь, которая может наблюдаться в спектрах молекул типа шарового волчка, линейных многоатомных молекул и двухатомных молекул, имеющих отличный от нуля спин в основном электронном состоянии.

Отсчет линий Р-ветви начинается с J = 1 (переход из ν” = 0, J” = 1 в ν’ = 1, J’ = 0), Линии R-ветви расположены со стороны больших волновых чисел от ν₀₀, а первая наблюдаемая линия соответствует переходу из ν " = 0, J” = 0 в ν’ = 1, J’ = 1.

Волновые числа переходов, соответствующих R-ветви, для которой J = J + 1, равны:

ν_R  =  ν₀₀ +F’(J’)-F”(J”) =  ν₀₀ + B’ ·(J + 1)(J +2) – B” ·(J + 1)J =

= ν₀₀ + 2B₀ + (3B’ - B”) J +  (B’ - B”)J²

Как принято в спектроскопии, величины, отмеченные двумя штрихами, относятся к исходному состоянию, отмеченные одним штрихом – к конечному состоянию. Вращательные квантовые числа для R-ветви принимают значения 0, 1,2...

Волновые числа переходов, соответствующих Р-ветви, для которой J’ = J” - 1, равны:

ν_P  =  ν₀₀ +F’(J’)-F”(J”) = ν₀₀ + B’ (J - 1)J – B” (J + 1)J =  ν₀₀ – (B’ + B”) J + (B’ - B”)J² ,

где В” и В’ – вращательные постоянные для состояний с ν = 0 и ν = 1, соответственно. Вращательные квантовые числа для Р-ветви принимают значения 1,2,3...

Поскольку разность (В’ – В” ) мала, то для малых J можно пренебречь взаимодействием колебаний с вращениями и принять В’ ~ В" ~ В. Тогда:

v_R=v₀₀ +2В + 2В·J, v_R=v₀₀ -2В·J

Таким образом, наблюдаемый спектр в первом приближении (жесткий ротатор) представляет собой серию равноотстоявших линий с расстояниями между ними, равными 2В.

Для нежесткого ротатора уровни вращательной энергии представляются в виде: