Определение момента инерции маятника Максвелла. Определение силы натяжения нитей при движении и в момент "Рывка" (нижняя точка траектории)

1. Цель работы: определение момента инерции маятника Максвелла. Определение силы натяжения нитей при движении и в момент "рывка" (нижняя точка траектории).

2. Теоретические основы работы.

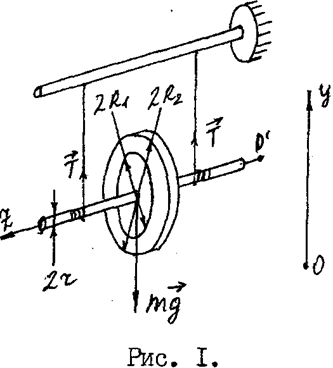Маятник Максвелла представляет собой однородный диск, насаженный на цилиндрический вал (рис. 1); центры масс диска и вала лежат на оси вращения. На вал радиусом r намотаны нити, концы которых закреплены на кронштейне. При разматывании нитей маятник Максвелла совершает плоское движение. Плоским называют такое движение, при котором все точки тела перемещаются в параллельных плоскостях. Плоское движение маятника можно представить как сумму двух движений - поступательного движения центра масс вдоль оси OY, со скоростью V и вращательного движения с угловой скоростью w относительно оси O’Z , проходящей через центр масс маятника.

Рис. 1

При движении маятника Максвелла происходит процесс перехода потенциаль­ной энергии в кинетическую и обратно. Разумеется, механическая энергия посте­пенно убывает в результате действия сил трения. Согласно теореме о движении центра масс, центр масс движется как материальная точка, масса которой равна массе системы, а действующая на нее сила - геометрической сумме всех внешних сил, действующих на систему:

åM_iZ = ma_c

Здесь индекс С означает центр масс системы.

Основное уравнение динамики вращательного движения для маятника максвелла относительно мгновенной оси O'Z, проходящей через центр масс имеет вид

åM_iZ = J_ZE_Z

Здесь J_Z - момент инерции маятника относительно оси O'Z.

Е_Z - проекция углового ускорения на ось O'Z; левая часть урав­нения - алгебраическая сумма моментов внешних сил относительно оси O'Z.

Если нить не проскальзывает, то скорость центра масс маятника и угловая скорость w связаны кинематическим соотношением

V_c = wr

а) Определение момента инерции маятника Максвелла.

Используя закон сохранения механической энергии можно экспери­ментально определить момент инерции маятника. Для этого измеряется время t опускания маятника массой m с высоты h.

Примем потенциальную энергию маятника Максвелла W_п.н. = 0 в поло­жении, когда маятник находится в нижней точке. Кинетическая энер­гия в этом положении

W_к.н. = mV²/2 + Jw²/2   (1)

Здесь V - скорость центра масс маятника; w - угловая скорость;

J - момент инерции маятника относительно оси, проходящей через центр масс: m = m_в + m_д + m_л - масса маятника; m_в, m_д,m_л - массы вала, диска и кольца, входящих в состав маятника. В верхнем положении маятника его потенциальная энергия

W_п.в. = mgh,

а кинетическая энергия равна нулю. Из закона сохранения механи­ческой энергии для маятника Максвелла (диссипативными силами, т.е. силами трения, сопротивления воздуха и т.п. пренебрегаем) следует

mgh = mV²/2 + Jw²/2   (2)

Так как центр масс маятника движется прямолинейно и равноус­коренно, то

h = at²/2; V = at   (3)

Из (3) получим  V= 2h/g   (4)

Подставляя соотношение (4) в (2) и используя соотношение между скоростью центра масс и угловой скоростью вращения маятника относительно оси симметрии, получим формулу для расчета эксперимен­тального момента инерции маятника Максвелла

J_э = mr²(gt²/2h – 1)   (5)

Здесь r – радиус вала

Полученный результат сравниваем со значением момента инерции, определяемым из теоретических соображений. Теоретический момент инерции маятника Максвелла можно рассчитать по Формуле

J_T = J_B + J_Д + J_K   (6)

Здесь J_B, J_Д, J_K - моменты инерции составных частей маятника: вала, диска и кольца соответственно. Используя общую формулу для определения момента инерции

J = ∫r²dm   (7)

найдем моменты инерции элементов маятника Максвелла.

JД = mДR12/2   (9)

Момент инерции вала J_B = m_вr₂/2   (8)

Момент инерции диска

Здесь R₁ - радиус диска, он же внутренний диаметр кольца (рис. 1). Момент инерции кольца

J_K = m_K*(R₁² + R₂²)/2   (10)

Здесь R₂ - внешний диаметр кольца

б) Определение силы натяжения нитей при движении маятника Максвелла Т_Д и в момент "рывка" – Т_Р.

Движение маятника Максвелла описывается системой уравнений

-ma = 2T – mg   (11); J_E = 2Tr   (12); h = at²/2   (13)

Из (11) и (12) следует, что при движении маятника Максвелла сила натяжения нити равна

T_Д = mg/2(mr²/J + 1)   (14)

где момент инерции маятника J определяется соотношением (5).